Skispringer springt vom Schanzentisch mit Winkel theta und Geschwindigkeit v

Question

Aufgabe:

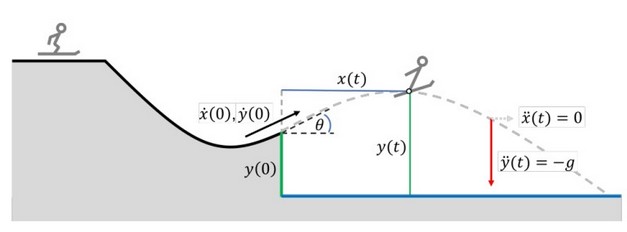
Ein Skispringer springt vom Schanzentisch mit Winkel $\theta$ und Geschwindigkeit $v$ ab. Folgende Differentialgleichungen beschreiben die vertikale und horizontale Beschleunigung des Skispringers zum Zeitpunkt $t$ (wir ignorieren alle externen Kräfte bis auf die Erdbeschleunigung $g \approx 9.81$)

$\begin{array}{l} \ddot{y}(t)=-g \\ \ddot{x}(t)=0 \end{array}$

Die Anfangsbedingungen (d.h. bei $t=0$ ) sind gegeben als die vertikale und horizontale Geschwindikeit
$\begin{array}{l} \dot{y}(0)=v \sin \theta \\ \dot{x}(0)=v \cos \theta \end{array}$

und die Höhe (und Distanz) beim Absprung
$\begin{array}{l} y(0)=h_{0} \\ x(0)=0 . \end{array}$

Lösen Sie diese Differentialgleichungen numerisch mit der Expliziten Euler Methode. Das heißt, Sie berechnen die Distanz $x$ und Höhe $y$ des Skispringers für die diskreten Zeiten $t_{0}, \ldots, t_{n}$ mit $t_{n}=t_{0}+n \cdot h$. Sie müssen dafür die Methode zweimal für jede Dimension anwenden um die Werte für $t_{n+1}$ zu bekommen. Zuerst, werden die Geschwindigkeiten $\dot{x}_{n+1}, \dot{y}_{n+1}$ von der Beschleunigung approximiert. Anschließend berechnen Sie die Distanz $x_{n+1}$ und Höhe $y_{n+1}$ aus den numerisch berechneten Geschwindigkeiten $\dot{x}_{n}, \dot{y}_{n}$.

a) (1 Punkt) Berechnen Sie per Hand die ersten zwei Zeitschritte $t_{1}=h, t_{2}=2 h$, mit $h=\frac{1}{4}$ mit der Expliziten Euler Methode. Berechnen Sie die Anfangswerte $\dot{x}_{0}, \dot{y}_{0}, x_{0}, y_{0}$ aus den folgenden Parameter
$h_{0}=1, \quad \theta=\frac{\pi}{4}, v=2 \sqrt{2}$
Zur Vereinfachung dürfen Sie für die Erdbeschleunigung $g=10 \mathrm{~m} / \mathrm{s}^{2}$ annehmen.

b) (1 Punkt) Implementieren Sie in Julia die Explizite Euler Methode um die erwähnten Differentialgleichungen zu lösen - siehe den Julia Code ski_jump_euler.jl.

c) (0.5 Punkte) Berechnen Sie für jeden Zeitschritt den Fehler zwischen der analytischen Lösung und dessen Approximation, z.B. für die vertikale Komponente $\left|y\left(t_{n}\right)-y_{n}\right|$.

d) (0.5 Punkte) Testen Sie ihre Implementierung mit verschiedenen Zeitschrittgrößen $h$. Was können Sie beobachten? Erklären Sie das Verhalten geometrisch.

Problem/Ansatz:

Dieses Beispiel bringt mich leider echt zum verzweifeln... Also bis jetzt hät ich mal (x(t), y(t)) = (v cos theta * t + C, -gt²/2 + v sin theta * t + D) wenn ich jetzt null einsetze würd ich sagen ist C = 0 und D = h0 leider beantwortet das nicht wirklich meine Aufgaben denk ich, weiter weiß ich aber auch leider nicht...

Comments

siehe den Julia Code ski_jump_euler.jl

Ich sehe ihn nicht.

---

ist nur der Code wo man die Euler Methode einfügt bzw das Ergebnis das sollte grundsätzlich für die Berechnung nicht relevant sein...

Answer 1

Hallo

du hast analytisch die Dgl richtig gelöst, aber das ist ja nicht die Frage, du sollst einfach Euler anwenden und numerisch lösen (um dann später die exakte Lösung mit der numerischen zu vergleichen)

erst 2 Schritte a) ohne Programm, dann b) mit dem Programm in das du offenbar nur das konkrete Problem eintragen musst

dann in c dein analytisches Ergebnis  mit dem Programmergebnissen vergleichen ,

Jetzt müsstest du sagen was dabei unklar ist?

lul

Comments

also wie approximiere ich die Geschwindigkeiten x n+1,  y n+1 von der Beschleunigung? ich weiß grundsätzlich wie man approximiert aber aber ich hab hier echt keinen plan wie wo und welche werte.

und wie berechne ich die Anfangswerte mit den Parametern da weiß ich leider auch echt nicht weiter....

---

Hallo

die Anfangswertw x'(0)=2√2cos(pi/4), y'(0)=2√2sin(pi/4)

x(0)=0, y(0)=1

die kannst du in deine analytischen Lösungen einsetzen  und  als  Amfangswerte in Euler einsetzen

x1=x(1*h)=x(0)+h*x'(0) (x'(1)=x'(0)+h*x''(0)  das  heißt ja x'(n*h)=x'(0

y1=y(1*h)=y(0)+h*y'(0) ; y'(1h)=y'(0)+h*y''(0)  mit y''(n*h)=-g für alle n

Gruß lul

---

danke! sorry für die weiteren Fragen, wie würde hier dann die Formel für den Zeitschritt t1 aussehen? Tue mir hier echt schwer... was wär außerdem bei c der Fehler zwischen analytisch und approximation?

---

hallo

den Schritt für t1=0+h hab ich doch hingeschrieben als x(h)=x(t1)

x(t2)=x(2h) usw.

Gruß lul