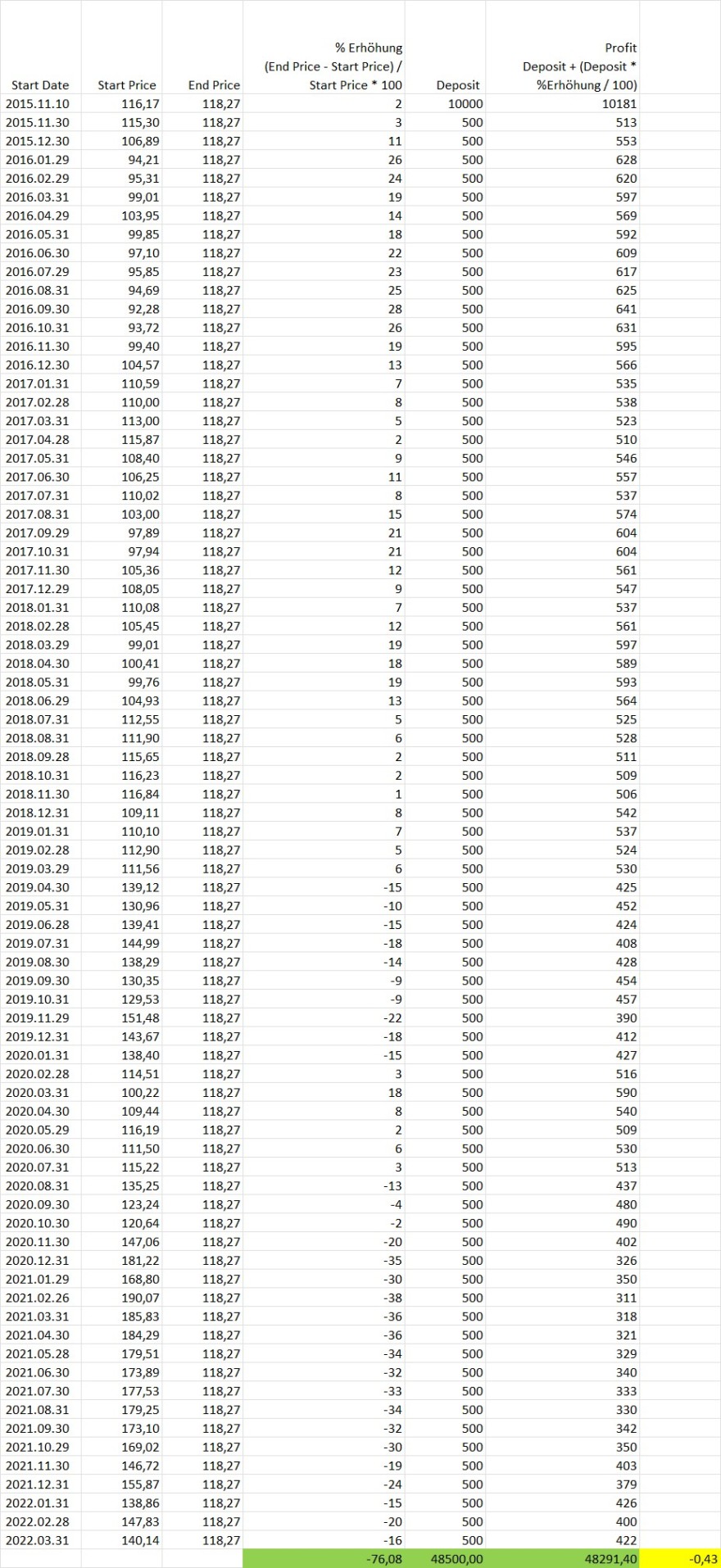
Hallo, ich habe einen ETF Sparplan in Excel simuliert. Mit Startkapital 10.000 EUR und monatlicher Einzahlung von 500 EUR. Das Ganze über ca. 6,5 Jahre. Bei jeder Einzahlung habe ich mir den aktuellen Preis des ETFs notiert und mittels des Endpreises die prozentuale Erhöhung des Preises berechnet. Den Gewinn und Verlust der einzelnen Einzahlungen von 10.000 EUR und die der 500 EUR habe ich dann mit Hilfe der prozentualen Erhöhung berechnet. In Summe wurden über die 6,5 Jahre 48.500 EUR eingezahlt und nach den 6,5 Jahren lag der Gesamtbetrag bei 48.291,40 EUR, dh ca. ein Verlust von 0,43%. Von der Preisentwicklung her passt das auch. Was ich nun nicht verstehe ist, wenn ich die einzelnen berechneten prozentualen Erhöhungen aufsummiere, dann hätte ich erwartet, dass hier auch -0,43% rauskommt. Es sind aber -76,08%? Wo liegt denn hier mein Denkfehler oder habe ich in der Berechnung einen Fehler gemacht? Herzlichen Dank!
Text erkannt:
48500,00