Aufgabe: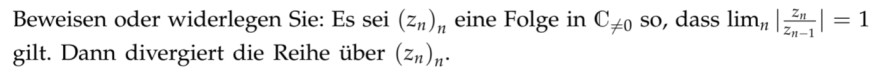
Text erkannt:
Beweisen oder widerlegen Sie: Es sei \( \left(z_{n}\right)_{n} \) eine Folge in \( \mathbb{C}_{\neq 0} \) so, dass \( \lim \limits_{n}\left|\frac{z_{n}}{z_{n-1}}\right|=1 \) gilt. Dann divergiert die Reihe über \( \left(z_{n}\right)_{n} \).
Problem/Ansatz: Mein Ansatz wäre jetzt zum widerlegen die Folge 1/n^2 zu nehmen und wollte fragen ob das richtig wäre?