Änderungsrate der Staulänge

Question

Aufgabe:

an einer Autobahnstelle wird die Stauentwickkung im Berufsverkehr untersucht. Aus den an einem bestimmten Tag erhobenen Messdaten wird die momentane Änderungsrate der staulänge durch die Funktion f mit der Gleichung

\(\displaystyle f(t)=\frac{3}{4} t^{3}-\frac{9}{2} t^{2}+6 t\quad,\quad 0 \leq t \leq 4 \)

modelliert ( \( t \) in Stunden, \( f(t) \) in Kilometern pro Stunde). Um 6:00 Uhr \( (t=0) \) beginnen sich die Fahrzeuge zu stauen. Der Graph von \( f \) ist in Abbildung 1 dargestellt.

a) Berechnen Sie die Nullstellen von f und erklären Sie die Bedeutung positivier und negativer Funktionswerte von f im Sachzusammenhang.

b) Bestimmen Sie rechnerisch die Zeitpunkte, zu denen die Staulänge am schnellsten zunimmt bzW. abnimmt.

c) (1) Begründen Sie, warum die Funktion F mit der Gleichung

\(\displaystyle F(t)=\frac{3}{16} t^{4}-\frac{3}{2} t^{3}+3 t^{2}\quad,\quad 0 \leq t \leq 4 \),

die Staulänge zum Zeitpunkt \( t \) beschreibt.

(2) Berechnen Sie die Staulänge für 6:30 Uhr.

(3) Berechnen Sie, um wie viel die Staulänge von 6:30 Uhr bis 7:00 Uhr zunimmt, und geben Sie für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge an.

(4) Bestimmen Sie den Zeitpunkt, zu dem die Staulänge ihr Maximum erreicht, und berechnen Sie diese maximale Staulänge.

d) An einem bestimmten Tag beginnt der Stau um 6:00 Uhr ( \( t=0 \) ) und hat sich um 10:00 Uhr \( (t=4) \) vollständig aufgelöst.

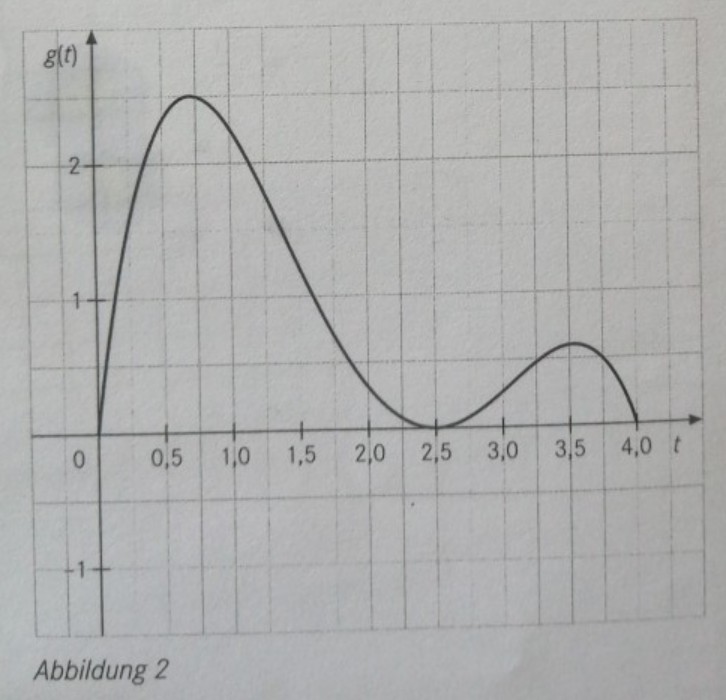
(1) Begründen Sie, warum es nicht möglich ist, die momentane Änderungsrate der Staulänge an diesem Tag durch die (differenzierbare) Funktion g zu modellieren, deren Graph in Abbildung 2 dargestellt ist.

(2) Ermitteln Sie eine notwendige Bedingung, die jede (differenzierbare) Funktion h, die die momentane Änderungsrate der Staulänge an diesem Tag sinnvoll modelliert, erfüllen muss.

Problem/Ansatz:

Textaufgaben sind zu schwer. Ich verstehe fast nichts. Bei a) Weiss ich wie man Nullstellen berechnet aber nicht wie man die Bedeutung negativer oder positiver funktionswerte in den sach Zusammenhang einordnen.

Bei b) wendepunkte berechnen und auch die Grenzen beachten also den y Wert des wendepunkte und die Grenzen in die ausgangsfunktion

C) verstehe ich nicht

(2) auch nicht

(3) leider auch nicht

(4) Extrema Berechnung

Comments

Ich habe mir erlaubt, die Textwüste etwas aufzuräumen. Da stand eine Zusammenstellung von Texten und Fotos von Texten, mit mehrmals denselben Passagen, die nicht wirklich lesefreundlich war. Vielleicht auch nicht für die Fragestellerin, denn sonst hätte sie auch zu Frage d) noch etwas geschrieben. Der Titel "Aufgaben sind zu schwer" war auch nicht aussagekräftig, das geht jedem Fragesteller so, sonst würden sie nicht hier vorbeikommen.

Answer 1

Bei a) Weiss ich wie man Nullstellen berechnet aber nicht wie man die Bedeutung negativer oder positiver funktionswerte in den sach Zusammenhang einordnen.

neg bedeutet: Staulänge nimmt ab, positiv Staulänge nimmt zu;

denn das f ist ja die ÄNDERUNGSRATE .

Bei b) wendepunkte berechnen und auch die Grenzen beachten also den y Wert des wendepunkte und die Grenzen in die ausgangsfunktion

NEIN! schnellste Zunahme der Staulänge liegt vor, wenn die

Änderungsrate maximal ist, hier also Extrema bestimmen.

c)   Die Ableitung von F ist gleich f, also ist F eine Funktion, deren

Änderungsrate durch f gegeben ist. Davon gibt es aber viele, nämlich

alle mit G(x) = F(x) + c.  Da aber um 6h erst der Stau beginnt und

6h ja t=0 bedeutet, muss F(0)=0 sein, also istz das angegebene F

diejenige Stammfunktion von f, bei der das stimmt.

Länge um 6:30h also F(0,5)

(3)  Zunahme:  F(1)-F(0,5)

mittlere Änderung (F(1)-F(0,5)) / (1-0,5)  .

(4) Maximum von F bestimmen ( mit F'(x)=0 etc. ... )

d) (1)  g ist nie negativ, also würde bei dieser Funktion die

Staulänge zwar zunehmen (positive Werte) aber nie abnehmen.

 (2)  Integral von 0 bis 4 muss gleich 0 sein.

Comments

Danke für die Antwort, dennoch sehe ich nur Hyroglyphen... Ich weiß zwar wie man Extrema, Wendepunkte etc. Berechnet aber sobald es um Kontext Aufgaben geht sehe ich den Wald vor lauter Bäumen nicht. Ich bin verzweifelt. Hast du vielleicht einen Tipp der mir helfen könnte? Ich habe mir auf Youtube "Vokabeln" für Analysis angeschaut, die helfen jedoch nicht besonders, es sei denn die Klausur wäre mega einfach.

---

Wenn die gegebene Funktion f eine momentane Änderungsrate ist,

geben die Werte, die man damit ausrechnet an, wie sich eine

Sache (hier die Staulänge) andert.

Das heißt: positive Werte bedeuten Zunahme

und negative Werte Abnahme ( der Staulänge).

Wird oft auch z.B. mit Wasserstand in einem Becken

oder Stausee oder so benutzt. Dann ist das das Gleiche:

Das heißt: positive Werte bedeuten Zunahme
und negative Werte Abnahme.

Schnellste Zunahme, also beim Maximum von f

Stagnation (kurzfristig keine Änderung) bei den

Nullstellen von f.  etc.

---

Vielen lieben Dank, jedoch muss ich dazu Anmerken, dass es tatsächlich nicht viel bringt, denn sobald eine andere Kontext Aufgabe ins Spiel kommt sehe ich Schwarz. Ich schaffe es aus irgendeinem Grund nicht "durchzublicken". Ich glaube das könnte einfach daran liegen, dass ich vielleicht von Natur aus einfach nicht begabt in Mathe bin

---

dass ich vielleicht von Natur aus einfach nicht begabt in Mathe bin

Sowas kann man sich einreden. Wenn man es lange genug tut, glaubt man es vielleicht sogar. Bringt aber nichts, selbst wenn es wahr wäre.

---

Aber ich lerne die ganze Zeit. ) :

Und ich war schon als Kind extrem schlecht in Mathe, ich kriege es irgendwie einfach nicht hin... Nach Konzept kann ich ja rechnen aber die textaufgaben sind für mich so als ob ich die nadel im Heuhaufen finden müsste