Funtionsgleichung einer Gerade bestimmen

Question

Aufgabe:

hallo ;

meine Aufgabe lautet :

Eine Gerade verlaeuft durch die Punkte P1(√2; 3) und P2(4; √3). Ermitteln Sie die Funktionsgleichung y(x) der Geraden

Problem/Ansatz:

wer kann mir dabei helfen , ich habe Problem bei der Gleichung !!!

hab am ende m= 3-b/√2 , aber ich konnte nicht weiter machen :!!!

Answer 1

y= m*x+b

m= (√3-3)/(4-√2) = ((√3-3)(4-√2))/(16-2) = z

3= z*√2+b

b= 3-z*√2

z darfst du ausrechnen. :)

Comments

was meinen Sie mit z , z gibts gar nicht in der Gleichung !!

:/

---

m= (√3-3)/(4-√2) = ((√3-3)(4-√2))/(16-2) = z

Er hat das, was der Anstieg m sein soll, am Ende als z bezeichnet.

Damit kannst du

z darfst du ausrechnen. :)

interpretieren als

m darfst du ausrechnen. :)

---

z ist eine Substitution um Schreiberei zu sparen.

Typische Quälaufgabe, damit man Fehler machen kann.

Reiner Sadismus bei solchen Aufgaben. Sehe das zum 1. Mal.

Zeitschinden durch rumrechnen lassen im Unterricht.

Schüler muss rechnen, Lehrer geht eine rauchen oder schaut zum Fenster raus.

Kenn ich noch aus meiner Zeit.

---

z ist eine Substitution um Schreiberei zu sparen.

m durch z zu ersetzen ist eine 1:1-Substitution. Die Schreibarbeit bleibt letztendlich die Gleiche. Sieht eher aus wie die Anpassung an Gewohntes.

Schüler muss rechnen,

Ja. Das Rationalmachen von Nennern ist eine gute Gelegenheit zur Anwendung der (30 mal wiederholten und immer wieder gern vergessenen) dritten binomischen Formel. Daran sehe ich nichts ehrenrühriges. Festigung erfolgt durch regelmäßíge Wiederholung.
Im ganzen Kollegium raucht bei uns übrigens nur noch einer von 50.

Answer 2

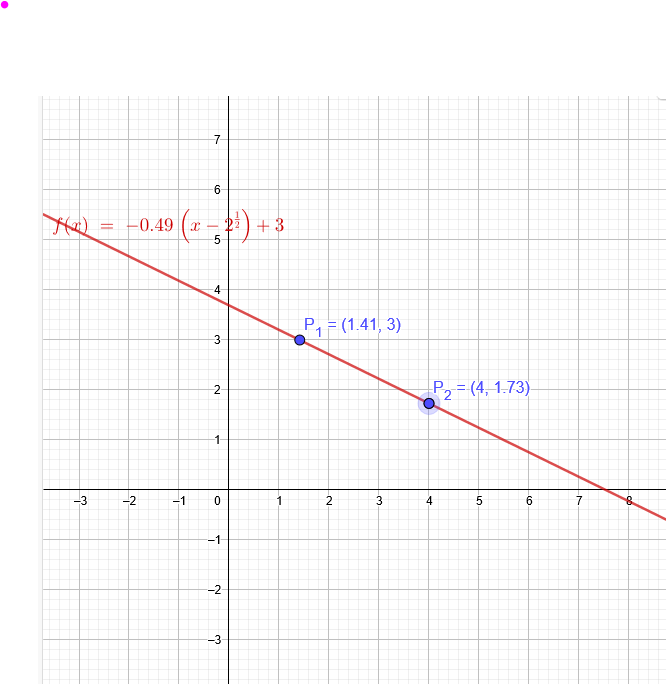
"Eine Gerade verläuft durch die Punkte \( P1( \sqrt{2}  | 3)\) und \(P2(4|  \sqrt{3}  )\). Ermitteln Sie die Funktionsgleichung \(y(x)\)der Geraden."

Geradengleichung durch 2 Punkte:

\( \frac{y₂-y₁}{x₂-x₁}=\frac{y-y₁}{x-x₁} \)

\( \frac{\sqrt{3} -3}{4-\sqrt{2}}=\frac{y-3}{x-\sqrt{2}} \)

\( \frac{y-3}{x-\sqrt{2}} =\frac{\sqrt{3} -3}{4-\sqrt{2}}≈-0,49\)

\( y(x) ≈-0,49*(x-\sqrt{2})+3\)

Comments

Nein, Moliets.

Das Verwenden von Näherungswerten ist hier sehr kontraproduktiv.

Die Zielrichtung der Aufgabe ist genau DAS nicht.

Ganz besonders lächerlich wird es, wenn du mit dem Faktor \((x-\sqrt{2})\) genaues Arbeiten vorgaukelst und das dann mit \("≈-0,49"\) peinlich zerstörst.