f(x) = 2·COS(x + π/10)·e^{- x/5}
f'(x) = - 2/5·e^{- x/5}·(COS(x + π/10) + 5·SIN(x + π/10))
Extremstellen f'(x) = 0
COS(x + π/10) + 5·SIN(x + π/10) = 0 | :5 : COS(x + π/10)
1/5 + SIN(x + π/10)/COS(x + π/10) = 0
TAN(x + π/10) = - 1/5
x = ARCTAN(- 1/5)
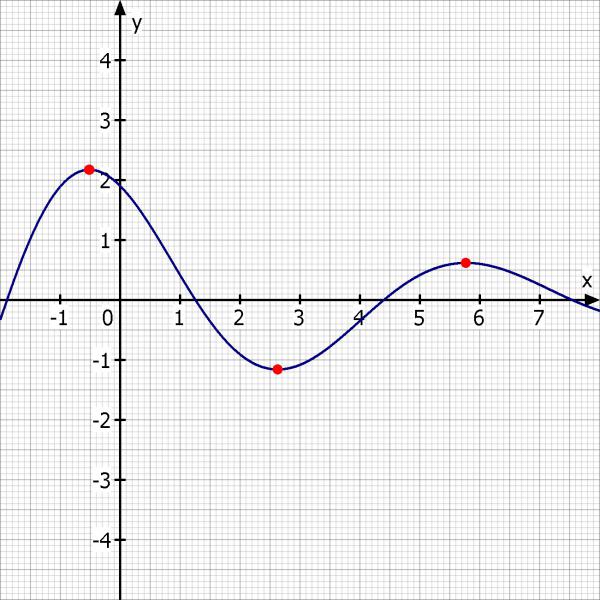
x1 = ARCTAN(- 1/5) - π/10 = -0.5115548252
x2 = ARCTAN(- 1/5) + 9/10·pi = 2.630037828
x3 = ARCTAN(- 1/5) + 19/10·pi = 5.771630481
Jetzt nur noch in die Ausgangsfunktion einsetzen
f(x) = 2·COS(x + π/10)·e^{- x/5}
f(-0.5115548252) = 2.172433111
f(2.630037828) = -1.158967193
f(5.771630481) = 0.6182951958
Skizze