Tangente und Berührpunkt?

Question

Aufgabe: Es wird die Funktion f betrachtet. Lege vom Punkt P aus die Tangenten an den Graphen von f. Stelle die Gleichung der Tangenten auf und nenne den Berührungspunkt. Als Aufgabe:

f(x)=-x^2+5, P(0/9)

Problem/Ansatz:

Ich bin völlig planlos. Hilfe und Weg wäre sehr hilfreich

Answer 1

Hallo,

allgmeine Form einer Tangentengleich y = mx + n

n = Schnittpunkt mit der y-Achse = 9

m = Steigung = 1. Ableitung

Nenne den gesuchten Punkt A (a|f(a))

\(f'(x)=-2x\\ f'(a)=-2a=m\)

Setze die Koordinaten von A in die Gleichung ein und löse nach a auf:

\(-a^2+5=-2a\cdot a+9\\ a^2=4\\ a=\pm2\)

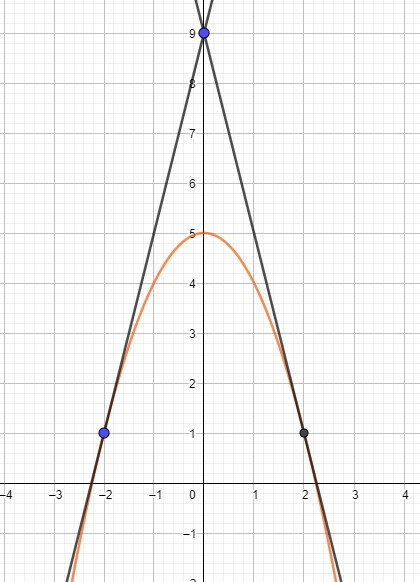
Gruß, Silvia

Comments

Danke!! Wie würde man dann die Gleichung der Tangente aufstellen ?

---

y = mx + n

n = 9

m = Steigung = 1. Ableitung

Setze also -2 bzw 2 in die 1. Ableitung ein.