Ansatz f(x) = ax*(x-6)^2 - Steckbriefaufgabe

Question

Aufgabe:

Hi,

mir ist leider nicht ganz klar, wie man bei er Funktion auf den Ansatz f(x) = ax*(x-6)^2 kommt.

Beid er Funktion handelt es sich um eine Funktion dritten Grades mit den Punkten (0/0), EP(2/4), WP(4/2) und EP(6/0).

Über Hilfe oder eine Erklärung wäre ich sehr dankbar, da ich das gerne verstehen würde.

Vielen Dank und viele Grüße!

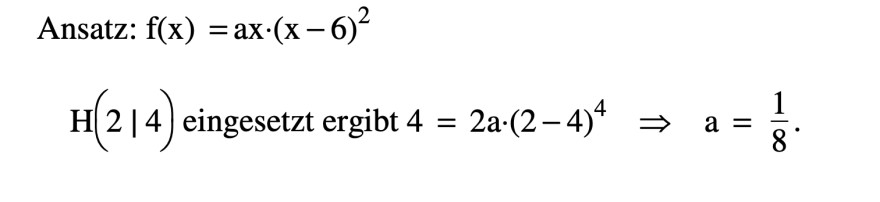
Text erkannt:

Ansatz: \( \mathrm{f}(\mathrm{x})=\mathrm{ax} \cdot(\mathrm{x}-6)^{2} \)
\( \mathrm{H}(2 \mid 4) \text { eingesetzt ergibt } 4=2 \mathrm{a} \cdot(2-4)^{4} \Rightarrow \mathrm{a}=\frac{1}{8} \text {. } \)

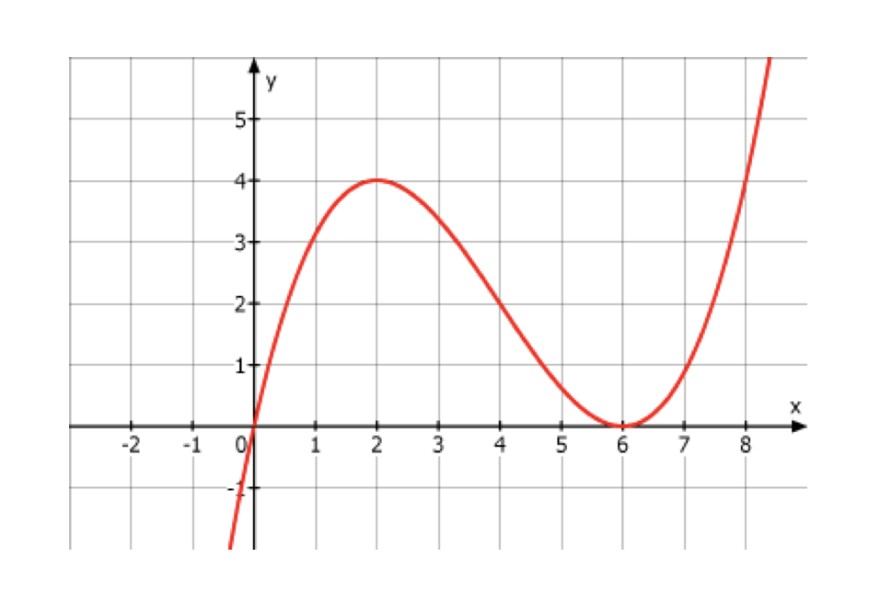
Problem/Ansatz:

Answer 1

Hallo,

wenn der Graph gegeben ist, siehst du die doppelte Nullstelle bei x = 6. Daher \((x-6)^2\).

Da es sich um eine Funktion 3. Grades handeln soll, wird die Klammer noch mit ax multipliziert.

Gruß, Silvia

Comments

Wieso zwei Nullstellen? Die Funktion berührt die x-Achse doch nur in einem Punkt für x=6

---

Genau, und deswegen auch die doppelte Nullstelle. Würde der Graph die x-Achse an dieser Stelle schneiden, wäre der Faktor nur (x - 6).

---

Aber wieso die doppelte nullstelle? :/

Das ist so ein bisschen mein Problem. Weil die Nullstelle als Tiefpunkt doppelt oder warum?

---

Weil die x-Achse nur berührt wird, nicht geschnitten.

---

Da es sich um eine Funktion 3. Grades handeln soll, wird die Klammer noch mit ax multipliziert.

Eine Funktion 3. Grades hat höchstens 3 reelle Nullstellen. Die dritte Nullstelle ist x=0 und deshalb ist x ein Linearfaktor des Funktionsterms.