Text erkannt:
\( f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=\lfloor x\rfloor \quad \) und \( \quad g: \mathbb{R} \rightarrow \mathbb{R}, g(x)=\frac{2}{2+e^{-2 x}} \)
Aufgabe:
Für eine reelle Zahl x ∈ R sei ⌊x⌋ ∈ Z die Abrundung von x, d.h., ⌊x⌋ ist die größte ganze Zahl
z ∈ Z mit z ≤ x. Betrachte die folgenden Funktionen:
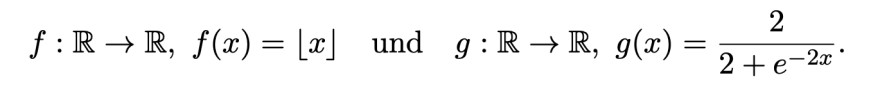
Untersuchen Sie, ob f , g und f ◦ g stetig sind
Ich komme leider nicht wirklich voran und wäre deshalb für jede Hilfe sehr dankbar!