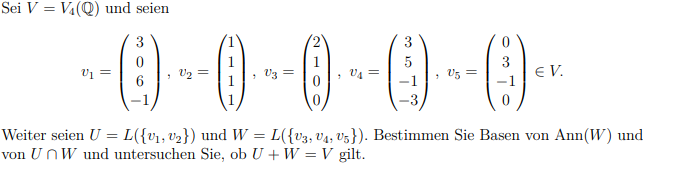
Text erkannt:
Sei \( V=V_{4}(\mathbb{Q}) \) und seien
\( v_{1}=\left(\begin{array}{c} 3 \\ 0 \\ 6 \\ -1 \end{array}\right), v_{2}=\left(\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}\right), v_{3}=\left(\begin{array}{l} 2 \\ 1 \\ 0 \\ 0 \end{array}\right), v_{4}=\left(\begin{array}{c} 3 \\ 5 \\ -1 \\ -3 \end{array}\right), v_{5}=\left(\begin{array}{c} 0 \\ 3 \\ -1 \\ 0 \end{array}\right) \in V . \)
Weiter seien \( U=L\left(\left\{v_{1}, v_{2}\right\}\right) \) und \( W=L\left(\left\{v_{3}, v_{4}, v_{5}\right\}\right) \). Bestimmen Sie Basen von \( \operatorname{Ann}(W) \) und von \( U \cap W \) und untersuchen Sie, ob \( U+W=V \) gilt.
ich hatte schon im letzten Blatt Probleme mit "Annullator", wusste nicht so wirklich was das sein sollte und von allem was die dim von nem Ann ist usw. und nein das auf wikipedia ist nicht so wirklich hilfreich :/
Daher eine Basis, bzw die Basen bon Ann(W) zu bestimmen werde ich ohne Hilfe nicht hinbekommen. die anderen 2 bekomme ich hin denke ich mal, ich möchte bloß mein Ansatz noch teilen und schauen ob der richtig ist:
U∩W=(v1,v2)∩(v3,v4,v5)
ich würde einfach v1=a*allen Vektoren von W überprüfen
dann v2=b* allen Vektoren von W überprüfen
-> was bei aber dann wäre U∩W={θ}
und bei U+W=V
U+W={v1,v2,v3,v4,v5}=V
V=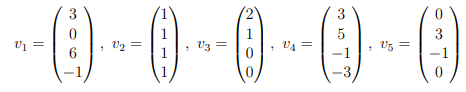
Text erkannt:
\( v_{1}=\left(\begin{array}{c}3 \\ 0 \\ 6 \\ -1\end{array}\right), v_{2}=\left(\begin{array}{l}1 \\ 1 \\ 1 \\ 1\end{array}\right), v_{3}=\left(\begin{array}{l}2 \\ 1 \\ 0 \\ 0\end{array}\right), v_{4}=\left(\begin{array}{c}3 \\ 5 \\ -1 \\ -3\end{array}\right), v_{5}=\left(\begin{array}{c}0 \\ 3 \\ -1 \\ 0\end{array}\right) \)