Problem/Ansatz:
Hey leute, ich komme bei der Aufgabe b) nicht wirklich weiter hat jemand eine Idee 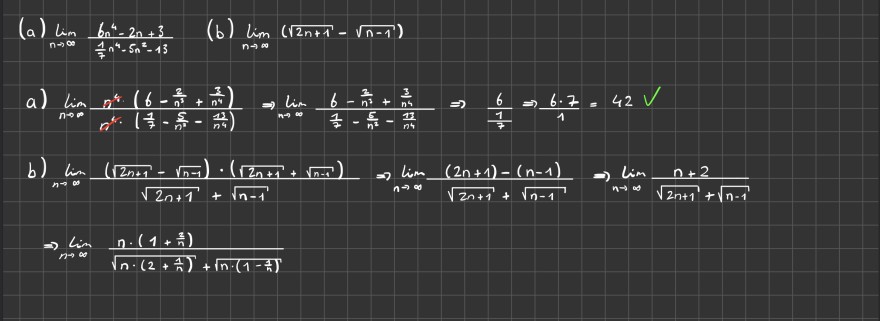
Text erkannt:
(a) \( \lim \limits_{n \rightarrow \infty} \frac{6 n^{4}-2 n+3}{\frac{1}{7} n^{4}-5 n^{2}-13} \)
(b) \( \lim \limits_{n \rightarrow \infty}(\sqrt{2 n+1}-\sqrt{n-1}) \)
a) \( \lim \limits_{n \rightarrow \infty} \frac{n^{4} \cdot\left(6-\frac{2}{n^{2}}+\frac{3}{n^{4}}\right)}{n^{4} \cdot\left(\frac{1}{7}-\frac{5}{n^{2}}-\frac{13}{n^{4}}\right)} \Rightarrow \lim \limits_{n \rightarrow \infty} \frac{6-\frac{2}{n^{2}}+\frac{3}{n^{4}}}{\frac{1}{7}-\frac{5}{n^{2}}-\frac{13}{n^{4}}} \Rightarrow \frac{6}{\frac{1}{7}} \Rightarrow \frac{6.7}{1}=42 \mathrm{~V} \)
b) \( \lim \limits_{n \rightarrow \infty} \frac{(\sqrt{2 n+1}-\sqrt{n-1}) \cdot(\sqrt{2 n+1}+\sqrt{n-1})}{\sqrt{2 n+1}+\sqrt{n-1}} \Rightarrow \lim \limits_{n \rightarrow \infty} \frac{(2 n+1)-(n-1)}{\sqrt{2 n+1}+\sqrt{n-1}} \Rightarrow \lim \limits_{n \rightarrow \infty} \frac{n+2}{\sqrt{2 n+1}+\sqrt{n-1}} \) \( \Rightarrow \lim \limits_{n \rightarrow \infty} \frac{n \cdot\left(1+\frac{2}{n}\right)}{\sqrt{n \cdot\left(2+\frac{1}{n}\right)}+\sqrt{n \cdot\left(1-\frac{1}{n}\right)}} \)