Muss nicht xs genau in der Mitte der x-Koordinaten von den zwei Punkten sein?

Question

Aufgabe: Stelle anhand dieser 2 Punkte eine passende quadratische Gleichung auf : P(1/1); P(3/1)

Problem/Ansatz: f(x)= a(x-xs) +ys

1= a(1-xs)+ys

Muss nicht xs genau in der Mitte der x-Koordinaten von den zwei Punkten sein? Weil ich weiß sonst nicht wie ich weitermachen soll.

Comments

Problem/Ansatz: f(x)= a(x-xs) +ys

Warum dieser Ansatz? War der vorgegeben? Naheliegend war doch eher$$(x-1)(x-3) +1= 1$$

~plot~ (x-1)(x-3) +1;1;{1|1};{3|1} ~plot~

---

Wie kommt man auf deine Nullstellenform? Kann man das nur so direkt aufstellen, wenn sie eine gemeinsame y-Koordinate haben?

---

Kann man das nur so direkt aufstellen, wenn sie eine gemeinsame y-Koordinate haben?

es geht auch, wenn die Y-Koordinaten unterschiedlich sind. Wird aber komplizierter. Das geht so in Richtung Newton-Interpolation. Aber es gibt immer unterschiedliche Ansätze

---

Ok, dann hab ich es jetzt verstanden. Dann hätte ich aber noch zwei Fragen:

1. Wie lautet die Funktionsgleichung für die in y Richtung verschobenen Normalparabel? Und wie kommt man darauf?

2. Wir haben heute auch noch darüber geredet, wie man xs mit einem angegebenen Punkt bei nach in x Richtung verschobenen Normalparabeln  berechnen kann.

Dann musste man mit dem Ergebnis von xs beurteilen, ob der Punkt auf dem linken oder rechten Zweig liegt. Woher weiß man aber wann er links und wann er rechts liegt?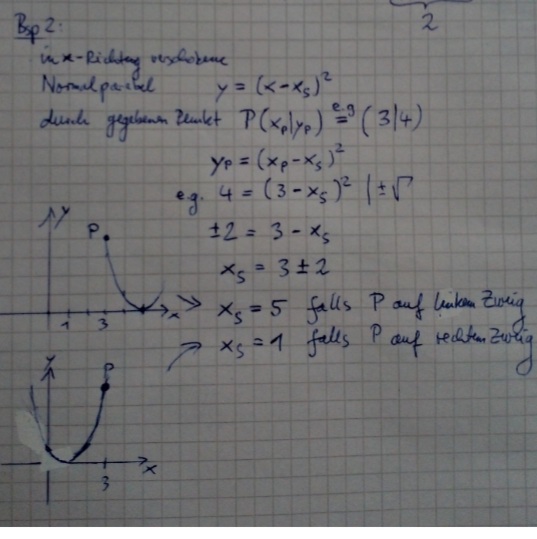

Text erkannt:

Bsp 2:
inx-Richtar mohoreac
Normelparial \( \quad y=\left(x-x_{5}\right)^{2} \)
duch gyebenen renkt \( P\left(x_{p} \mid y_{p}\right) \stackrel{\text { e.g }}{=}(3 / 4) \)

---

1. Wie lautet die Funktionsgleichung für die in y Richtung verschobenen Normalparabel? Und wie kommt man darauf?

wie kommt man darauf? Na ja - bei einer Funktion wie \(y=f(x)\) liefert \(f(x)\) den Y-Wert. Wenn man den um einen Wert \(b_0\) verschieben möchte, so addiere ihn doch $$y_2=f(x)+b_0$$ Macht doch irgendwie Sinn - oder? Damit verschiebt sich die ganze Funktion um \(b_0\) in Y-Richtung. Das gilt für jeden Typ von Funktion.

.. wie man x_s mit einem angegebenen Punkt bei nach in x Richtung verschobenen Normalparabeln berechnen kann. ... Woher weiß man aber wann x_s links und wann x_s rechts liegt?

gar nicht! beide Lösungen sind möglich. Vorausgesetzt sie werden nicht durch eine zusätzliche Bedingung in der Aufgabenstellung eingeschränkt. Es ist nichts ungewöhliches, dass es bei Problemen - gleich welcher Art - mehr als eine Lösung gibt.

Answer 1

Ja.

y=a(x-2)²+ys

(3|1) → 1=a(3-2)²+ys → 1=a+ys → ys=1-a

y=a(x-2)²+1-a

Comments

Danke, aber wie kommt man auf 1= a + ys? Wie stellt man das um?

---

Setz x=3 ein.

(3-2)²=1²=1

---

Vielleicht sollte man zunächst fragen ob ihr vielleicht eine Gleichung für eine verschobene Normalparabel mit a = 1 aufstellen sollt.

Wenn man die Parabel in Abhängigkeit von a aufstellen soll, dann würde sowas auch sicher in der Aufgabenstellung stehen. Es wäre zumindest ungewöhnlich wenn nicht.

Ansonsten gilt für den Punkt (3 | 1) einfach

f(3) = 1
a(3 - 2) + ys = 1
a + ys = 1
ys = 1 - a

Ist das so klar?

Answer 2

Zwischen x= 1 und x= 3 liegt x=2 in der Mitte.

-> Scheitel S(2/?)

Answer 3

P(1/1); P(3/1)
Aufgabe: Stelle anhand dieser 2 Punkte eine passende quadratische Gleichung auf : P(1/1); P(3/1)

Eine eindeutig bestimmbare quadratische
Gleichung benötigt 3 Punkte

Bei 2 Punkten gibt es unendliche viele Funktionen.

Du brauchst aber nur 1 ( eine ) anzugeben
Es steht dir frei welche.