Aufgabe:
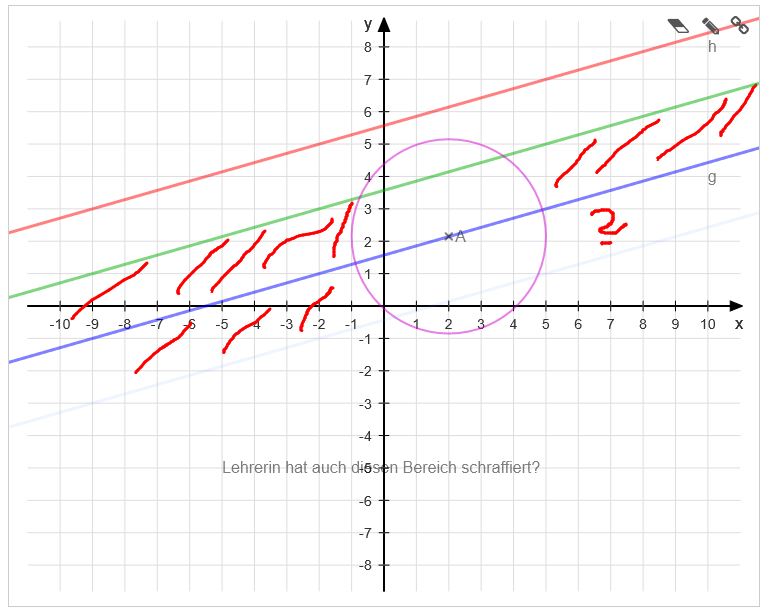
Konstruiere ein bieliebiges Parallelenpaar g und h, so dass gilt: d(g|h)=2cm. Markiere einen beliebigen Punkt auf g: A € g.
Markiere weiterhin aufgrund einer Konstruktion den Bereich farbig, in dem alle Punke P liegen, für die zugleich gilt:
d(P|g)<d(P|h) und d(P|A)>3cm
Problem/Ansatz:
Konstruktion g und h ist ok...Kann mir jemand helfen mit der Schraffierung? Zuerst hatte ich nur den Bereich oberhalb g schraffiert...aber unterhalb g bis zur halbtransparenten Gerade muss auch schraffiert werden, oder? (Bereich mit rotem Fragezeichen).
Die Lehrerin hat in der Lösung auch den Bereich unterhalb der halbtransparenten Gerade schraffiert.
Das würde ja nur stimmen, wenn d ein Vorzeichen hat? Ist das der Fall oder ist d immer positiv...also ein Betrag?