Wie viele verschiedene Würfel kann man aus 6 Farben herstellen?

Question

Aufgabe:

Ein Würfel werde mit 6 voneinander verschiedenen Farben bemalt. Wie viele unterschiedliche
Würfel kann man fertigen?
Lösung: Man kann insgesamt 30 verschiedene Würfel fertigen

Problem/Ansatz:

mein Ansatz: Reihenfolge wichtig, ohne Wiederholung (verschiedene Farben) -> also Variation ohne Wiederholung

(n über k) * k! = (6 über 6) * 6! = 720 Möglichkeiten

Leider komme ich (trotz Ausprobieren) an dieser Stelle nicht weiter

Comments

Es steht ja nirgends, dass die Würfelseiten von 1 bis 6 beschriftet sind.

---

Warum sollte das da stehen müssen ?

---

Damit die Lösung 720 ist :-)

Answer 1

Die vordere Seite kann eine von 6 Seiten des Würfels sein.

Ist festgelegt, welche Seite vorne liegt, dann kann die obere Seite eine von 4 Seiten sein.

Durch Angabe von vorderer Seite und oberer Seite ist die Lage des Würfels deshalb eindeutig festgelegt. Es gibt somit 6·4 = 24 mögliche Lagen, in denen der Würfel liegen kann.

(n über k) * k! = (6 über 6) * 6! = 720 Möglichkeiten

Soweit richtig. Dabei wird aber nicht berücksichtigt, dass je 24 dieser Möglichkeiten identisch sind, wenn die Seiten des Würfels nicht unterschieden werden können.

Answer 2

Hallo,

der Würfel kann ja in verschiedenen Positionen liegen.

Die Farben nenne ich 1,2,...,6; Die Flächen G(rundfläche), D(eckfläche), V(orne), R(echts), H(inten), L(inks).

Die erste Farbe packe ich nach unten: G → 1

Die zweite Farbe kann jetzt auf einer Seitenfläche oder auf der Deckfläche sein.

-- V → 2

Dann gibt es für die restlichen vier Seiten 4!=24 Möglichkeiten.

-- D -->2

Eine beliebige Seitenfläche kann nun mit Farbe 3 versehen werden. Für die anderen drei gibt es 3!=6 Möglichkeiten.

4!+3!=30

:-)

Comments

Auch vielen Dank:) habe es durch einen Mix der Antworten verstanden:)

Answer 3

Angenommen, die Farbe blau ist dabei. Du kannst dann den Würfel immer so drehen, dass du die blaue Fläche direkt von vorn ansiehst:

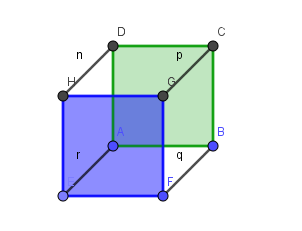
Für die dahinter liegende Fläche gibt es jetzt 5 verschiedene Möglichkeiten (hier eine Fläche als Beispiel grün dargestellt).

Nun gibt es noch 4 weitere Farben, eine davon sei jetzt rot:

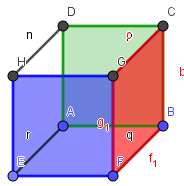
Die rote Fläche kann zwar jetzt links, oben, rechts oder unten sein, aber sie hat mit Sicherheit eine dieser 4 Lagen.

Du kannst den Würfel so drehen, dass die zuerst gewählte Farbe (hier blau) vorn bleibt und die dritte Fläche (hier rot) rechts ist.

In dieser Lage gibt es 3 Möglichkeiten, welche Farbe die obere Fläche bekommt, und danach zwei Möglichkeiten, welche Farbe die linke Flöche bekommt. (Die untere Fläche muss nehmen, was übrig bleibt).

Fazit: 5*(3*2)=30.

Comments

Auch vielen Dank:) habe es durch einen Mix der Antworten verstanden:)

Answer 4

Eine Ergänzung zu Oswalds Lösung:

Die Drehgruppe des Würfels ist isomorph zu \(S_4\)

und die hat \(4!=24\) Elemente.

Diese Gruppe operiert auf der Menge der

\(6!\) möglichen Verschieden-Färbungen von 6 Elementen

mit 6 Farben.

Die Anzahl der Bahnen ist dann \(6!/4!=5\cdot 6=30\).

Comments

Auch vielen Dank:) habe es durch einen Mix der Antworten verstanden:)