Hallo,
die Kurve sieht so aus:
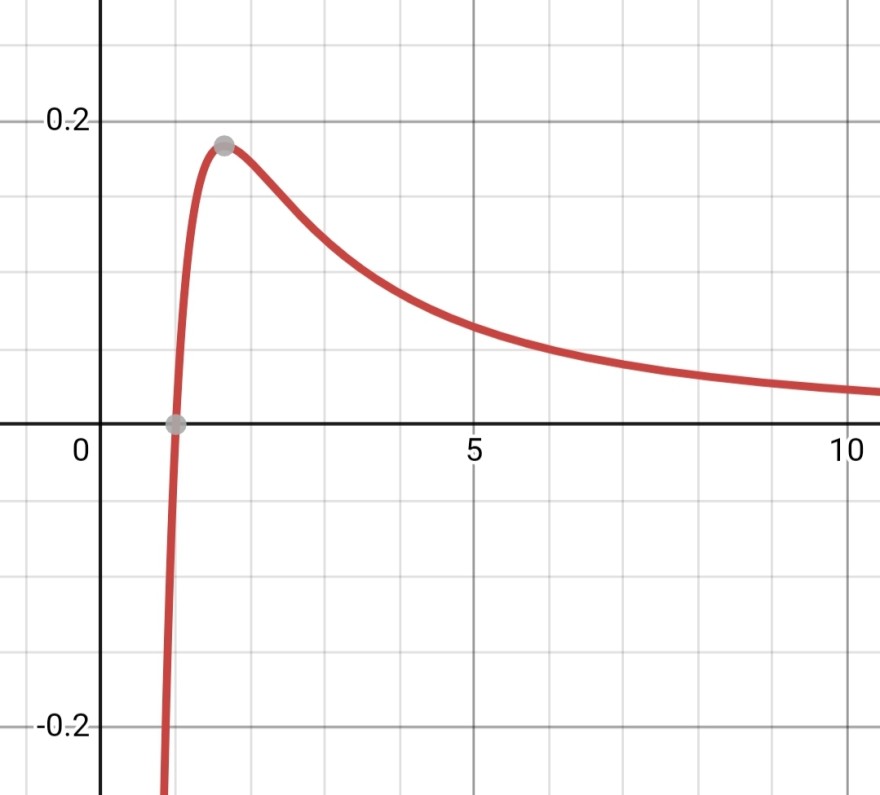
Nun ist die Frage, wie du auf diesen Verlauf kommen kannst.
Die Nullstelle ist klar.
Das Extremum liegt bei x=√e≈√(2,71828).
e liegt zwischen 2,56=1,6² und 2,89=1,7².
√e liegt also zwischen 1,6 und 1,7.
0,5/e≈0,5/2,7≈0,5/2,5=0,2
Da 2,7>2,5 gilt, ist 0,5/e<0,2.
Wenn du weißt, dass 27•37=999 ist, kannst du auch so rechnen:
0,5/2,7=(5•37)/(27•37)=185/999≈0,185
--> E(1,65|0,185)
Das stimmt erstaunlich gut mit dem genauen Wert überein.
Die Wendestelle muss zwischen 1,65 und 2,7 liegen, da e^{0,5}<e^{0,833}<e^1 gilt.
:-)