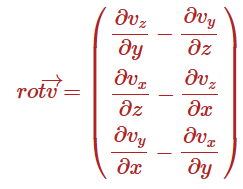a) Zeigen Sie, dass für z = f(x, y) = ln(√x+√y) die Gleichung ... erfüllt ist
∂x∂z= 2x(x+y)1
∂y∂z= 2y(x+y)1
einsetzt in:
x⋅∂x∂z+y⋅∂y∂z=21
x 2x(x+y)1 + y 2y(x+y)1 =21
2(x+y)1⋅(xx+yy)=1/2
2(x+y)1⋅(x⋅xx⋅x+y⋅yyy)=21
21 =21
b) Berechnen Sie die Rotation, rot v, des Vektorfeldes v : R3 → R3