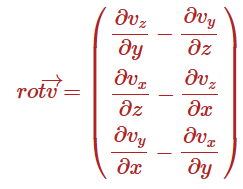Rechnungen und Definitionen

Question

Aufgabe:

a) Zeigen Sie, dass für z = f(x, y) = ln(√x+√y) die Gleichung

\( x \cdot \frac{\partial z}{\partial x}+y \cdot \frac{\partial z}{\partial y}=\frac{1}{2} \) erfüllt ist.

b) Berechnen Sie die Rotation, rot v, des Vektorfeldes v : R³ → R³, definiert durch

\( v(x, y, z):=\left(\begin{array}{c}2 x y^{2}+4 z^{3} \\ 2 x^{2} y \\ 12 x z^{2}\end{array}\right) \)

Problem/Ansatz:

ich verstehe leider absolut nicht wie ich hier verfahren soll und möchte fragen ob jemand mir bitte Rechen- und Lösungswege dieser Aufgaben schildern könnte. Ich bedanke mich vielmals im Voraus, mfg

Answer 1

a) Zeigen Sie, dass für z = f(x, y) = ln(√x+√y) die Gleichung ... erfüllt ist

\( \frac{\partial z}{\partial x} \)= \( \frac{1}{2 \sqrt{x}(\sqrt{x}+\sqrt{y})} \)

\( \frac{\partial z}{\partial y} \)= \( \frac{1}{2 \sqrt{y}(\sqrt{x}+\sqrt{y})} \)

einsetzt in:

\( x \cdot \frac{\partial z}{\partial x}+y \cdot \frac{\partial z}{\partial y}=\frac{1}{2} \)

x   \( \frac{1}{2 \sqrt{x}(\sqrt{x}+\sqrt{y})} \)  + y  \( \frac{1}{2 \sqrt{y}(\sqrt{x}+\sqrt{y})} \) =\( \frac{1}{2} \)

\( \frac{1}{2(\sqrt{x}+\sqrt{y})} \cdot\left(\frac{x}{\sqrt{x}}+\frac{y}{\sqrt{y}}\right)=1/2 \)

\( \frac{1}{2(\sqrt{x}+\sqrt{y})} \cdot\left(\frac{x \cdot \sqrt{x}}{\sqrt{x} \cdot \sqrt{x}}+\frac{y\sqrt{y}}{\sqrt{y} \cdot \sqrt{y}}\right)=\frac{1}{2} \)

\( \frac{1}{2} \) =\( \frac{1}{2} \)

b) Berechnen Sie die Rotation, rot v, des Vektorfeldes v : R3 → R3

Answer 2

Zeigen Sie, dass für z = f(x, y) = ln(√x+√y) die Gleichung\( x \cdot \frac{\partial z}{\partial x}+y \cdot \frac{\partial z}{\partial y}=\frac{1}{2} \)

Das heißt:

Bilde die partielle Ableitung von z nach x.

Hast du?

Multipliziere den erhaltenen Ableitungsterm mit x und notiere den Ergebnisterm.

Das heißt weiter:

Bilde die partielle Ableitung von z nach y.
Hast du?
Multipliziere den erhaltenen Ableitungsterm mit y und notiere den Ergebnisterm.

Das heißt final: Addiere die beiden notierten Terme und stelle (eventuell nach leichteren Termumformungen/Zusammenfassungen) erstaunt fest, dass diese Summe 1/2 ergibt.

Wie sehen deine diesbezüglichen Zwischenergebnisse aus?

Comments

Hallo, vielen Dank für die Hilfe schonmal. Leider bin ich trotzdem zu verwirrt zu verstehen wie die ganzen Schritte aussehen sollen :( Könnten sie mir das ausnahmsweise alles mal darstellen dann kann ich es besser nachvollziehen könnte? Nur wenn es keine Umstände bereitet.