Optimierung: Behältermenge

Question

Text erkannt:

D
B
C
A

Wenn ich ein Werkstück (grün) habe, das von der Länge (D) her minimal länger ist als die Behälterlänge (blau, B), passt es normalerweise nicht in den Behälter. Nun kann man das Werkstück aber rotieren, sodass es doch in den Behälter passt. Durch die Drehung wird das Werkstück ja quasi in der Länge reduziert, während es in der Breite zunimmt. Kann mir jemand erklären, wie ich den optimalen Rotationswinkel sowie die theoretisch maximale Behältermenge ermitteln könnte?

LG

Comments

maximale Behältermenge ?

Definiere optimal

---

Definiere Behältermenge, bitte.

---

Statt Behältermenge meinst du wohl Behälterlange.

Ist ein Querschnitt des Werkstücks ein Rechteck? Welche Abmessungen hat es?

Ist der Behälter rechteckig? Welch Abmessungen hat er?

---

Behälter + Werkstück sind rechteckig. Ich hatte keine Zahlen angegeben, da es mir mehr um die Formel ging. Ziel ist es herauszufinden wie viele Werkstücke maximal in den Behälter passen, wofür man, meiner Meinung nach, eine möglichst geringe Rotation des Werkstücks benötigt, um die Werkstücke platzsparend ausrichten zu können.

Beispielwerte wären:

A=265mm

B=346mm

C=50mm

D=350mm

---

Was ist A, B, C, D Bezogen auf Werkstück und Behälter? Sollen es mehrere Werkstück sein, die nebeneinander in den Behälter passen sollen?

---

A ist die Breite des Behälters (horizontal), B die Länge (vertikal), C ist die Breite des Werkstücks und D die Länge. Es sollen so viele Werkstücke wie möglich nebeneinander gelegt werden.

---

Hm,

ich weiß nicht, wo es da was zu optimieren gibt.

Das Werkstück muß gerade soweit gedreht werden das es reinpasst und dann passen noch so viele Werkstücke daneben wie geht. Das kann man berechnen aber zu optimieren gibt es da nix, meine ich...

---

Mit den von die genannten Maßen passt genau ein Werkstück in den Behälter: Maßstabstreue Skizze war falsch. Siehe Kommentar von Wächter

---

Also ich würde schon 2 Stück unterbringen wollen

---

Wurde hier nicht grundsätzlich die Diagonale "CF", auf Basis der in dieser Zeichnung festgelegten Bezeichnungen, so weit rotiert, dass man ein Dreieck mit der Hypotenuse "CF" und der Höhe H=346mm (also der Höhe des Behälters) erhält? Könnte man sich nicht damit weitere Dreiecke erschließen?

---

Die Diagonale CF ist invariant. Es handelt sich ja nicht nur um eine einfache Drehung, sondern um eine affine Abbildung, das Teil muß ja auch verschoben werden. Ob man daraus eine geschlossene Formel bauen kann hab ich nicht versucht - vermutlich würde das auf eine Iteration hinaus laufen...

Answer 1

Ich hab mein Model mal durchgerechnet

H=346mm
B=50mm
L=350mm

die koordinaten von C wären

\(\displaystyle \left\{ x = \frac{B \; L \; H+ L^{2} \; \sqrt{B^{2} + L^{2} - H^{2}}}{B^{2} + L^{2}},\, y = \frac{-B \; L \; \sqrt{B^{2} + L^{2} - H^{2}} + L^{2} \; H}{B^{2} + L^{2}} \right\} \)

musst Du nur noch den Sägezahn entlang iterieren...

Comments

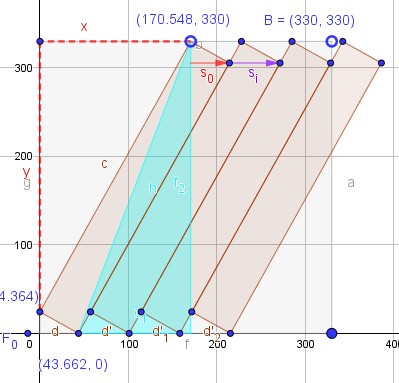
Zur Wahl von x,y siehe Bild:

Der Sägezahn wird doch etwas aufwändig

\( \frac{B^{3} \; H^{2} + 2 \; B^{3} \; L^{2} - B^{3} \; T \; \sqrt{B^{2} - H^{2} + L^{2}} + B^{2} \; H \; L \; T + 3 \; B^{2} \; H \; L \; \sqrt{B^{2} - H^{2} + L^{2}} - 3 \; B \; H^{2} \; L^{2} + 2 \; B \; L^{4} - B \; L^{2} \; T \; \sqrt{B^{2} - H^{2} + L^{2}} + H \; L^{3} \; T - H \; L^{3} \; \sqrt{B^{2} - H^{2} + L^{2}}}{B^{5} + 2 \; B^{3} \; L^{2} + B \; L^{4}}\)

kStapel(B,L,H,T)=(B^3 H^2 + 2B^3 L^2 - B^3 T sqrt(B^2 - H^2 + L^2) + B^2 H L T + 3B^2 H L sqrt(B^2 - H^2 + L^2) - 3B H^2 L^2 + 2B L^4 - B L^2 T sqrt(B^2 - H^2 + L^2) + H L^3 T - H L^3 sqrt(B^2 - H^2 + L^2)) / (B^5 + 2B^3 L^2 + B L^4)

kStapel(50,350,346,265)=2.85

kStapel(50,350,346,330)=4.07

kStapel(50,350,330,330)=3.022