Aufgabe:
Finde eine orthogonale Basis aus den folgenden drei Vektoren im Raum :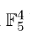
Text erkannt:
\( \mathbb{F}_{5}^{4} \)

Text erkannt:
\( \left\langle\left(\begin{array}{l}1 \\ 1 \\ 1 \\ 1\end{array}\right),\left(\begin{array}{l}1 \\ 2 \\ 3 \\ 1\end{array}\right),\left(\begin{array}{l}1 \\ 4 \\ 0 \\ 3\end{array}\right)\right\rangle \)
Problem/Ansatz:
Im Folgenden habe ich auch schon die Lösungen. Nun verstehe ich zwar wieso wir nicht GramSchmidt anwenden können (da wir und im Modulo 5 Raum befinden) aber verstehe NICHT wie man auf die Gleichung (gelbunterstrichen) kommt.

Text erkannt:
3. Call the generating vectors \( u_{1}, u_{2}, u_{3} \). Notice that
\( \left(\begin{array}{lll} 1 & 1 & 1 \\ 1 & 2 & 4 \\ 1 & 3 & 0 \\ 1 & 1 & 3 \end{array}\right) \underset{I I-I}{\stackrel{I I-I, I V-I}{\longrightarrow}}\left(\begin{array}{ccc} 1 & 1 & 1 \\ 0 & 1 & 3 \\ 0 & 2 & -1 \\ 0 & 0 & 2 \end{array}\right) \)
therefore \( u_{1}, u_{2}, u_{3} \) are linearly independent. Now we construct the orthogonal basis (notice that we can't use Gram-Schimdt). Fix \( v_{1}=u_{1}=(1,1,1,1) \), we are looking for a vector orthogonal to \( v_{1} \) of the form \( a(1,1,1,1)+b(1,2,3,1)+c(1,4,0,3) \), which give us the equation
\( 4 a+2 b+3 c=0 \)
We can take as a solution \( a=1, b=4, c=1 \) and we obtain the vector \( v_{2}=(1,3,3,3) \). Now we are looking for a vector orthogonal to \( v_{1} \) and \( v_{2} \) always of the form \( a(1,1,1,1)+ \) \( b(1,2,3,1)+c(1,4,0,3) \), which give us the system
\( \left\{\begin{array}{l} 4 a+2 b+3 c=0 \\ 4 b+2 c=0 \end{array}\right. \text {. } \)
We can take as a solution \( a=1, b=1, c=3 \) and we obtain the vector \( v_{3}=(0,0,4,1) \). It's easy to check that \( v_{1}, v_{2}, v_{3} \) are also linearly independent, so they form an orthogonal basis,