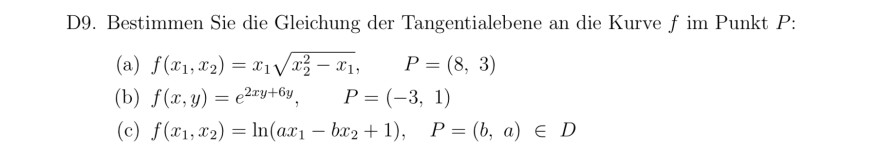
Text erkannt:
D9. Bestimmen Sie die Gleichung der Tangentialebene an die Kurve \( f \) im Punkt \( P \) :
(a) \( f\left(x_{1}, x_{2}\right)=x_{1} \sqrt{x_{2}^{2}-x_{1}}, \quad P=(8,3) \)
(b) \( f(x, y)=e^{2 x y+6 y}, \quad P=(-3,1) \)
(c) \( f\left(x_{1}, x_{2}\right)=\ln \left(a x_{1}-b x_{2}+1\right), \quad P=(b, a) \in D \)
Aufgabe:
Problem/Ansatz:
Kann mir jemand bei C) helfen?
Danke!