Zwischen der Funktion \(y= e^{\frac{1}{2}x} \) und der x-Achse wird im Intervall \((0;5]\) ein Rechteck
eingeschrieben. (Angaben in cm)
a)
Berechne Länge und Breite des Rechtecks, sodass die Fläche maximal wird.
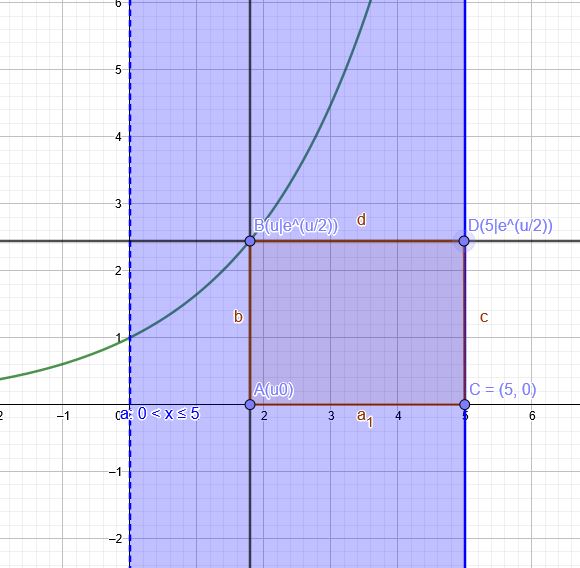
\(A(u)=(5-u) \cdot e^{\frac{1}{2}u} \) soll maximal werden.
\(A´(u)=(-1) \cdot e^{\frac{1}{2}u}+(5-u)\cdot e^{\frac{1}{2}u}\cdot \frac{1}{2} \)
\(- e^{\frac{1}{2}u}+(5-u)\cdot e^{\frac{1}{2}u}\cdot \frac{1}{2}=0 \)
\( e^{\frac{1}{2}u} \cdot(-1+(5-u)\cdot \frac{1}{2})=0 \)
1.)\( e^{\frac{1}{2}u} ≠0 \)
2.)\( (-1+(5-u)\cdot \frac{1}{2})=0 \)
\( u=3 \)