Text erkannt:
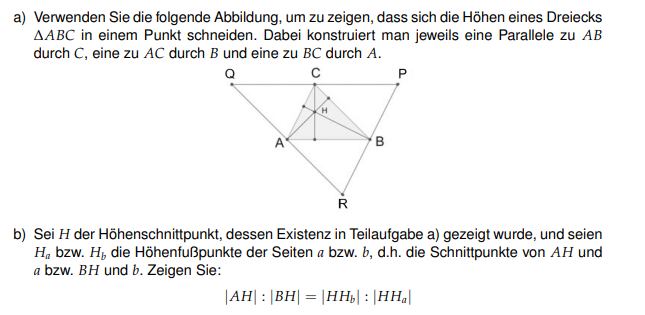
a) Verwenden Sie die folgende Abbildung, um zu zeigen, dass sich die Höhen eines Dreiecks \( \triangle A B C \) in einem Punkt schneiden. Dabei konstruiert man jeweils eine Parallele zu \( A B \) durch \( C \), eine zu \( A C \) durch \( B \) und eine zu \( B C \) durch \( A \).
b) Sei \( H \) der Höhenschnittpunkt, dessen Existenz in Teilaufgabe a) gezeigt wurde, und seien \( H_{a} \) bzw. \( H_{b} \) die Höhenfußpunkte der Seiten \( a \) bzw. \( b \), d.h. die Schnittpunkte von \( A H \) und \( a \) bzw. \( B H \) und \( b \). Zeigen Sie:
\( |A H|:|B H|=\left|H H_{b}\right|:\left|H H_{a}\right| \)
Hallo ich komme bei Aufgabenteil b irgendwie nicht weiter, ich habe auch keinen wirklichen Ansatz, kann mir wer helfen?