Aufgaben zur Binomialentwicklung

Question

Problem/Ansatz:

Text erkannt:

Sei \( x \in \mathbb{R} \) fest gewählt.
(a) Zeigen Sie mit Hilfe der Binominalentwicklung von \( \left(1+\frac{x}{n}\right)^{n} \), dass
\( \left(1+\frac{x}{n}\right)^{n}-\sum \limits_{k=0}^{n} \frac{x^{k}}{k !}=\sum \limits_{k=0}^{n}\left[\left(1-\frac{1}{n}\right) \cdots\left(1-\frac{k-1}{n}\right)-1\right] \frac{x^{k}}{k !} . \)
(b) Sei \( \varepsilon>0 \). Da \( \sum \frac{x^{k}}{k !} \) absolut konvergiert, gibt es ein \( N \in \mathbb{N} \operatorname{mit} \sum \limits_{k=N+1}^{\infty} \frac{|x|^{k}}{k !}<\frac{\varepsilon}{2} \). Zeigen Sie, dass für \( n \rightarrow \infty \)
\( \sum \limits_{k=0}^{N}\left[\left(1-\frac{1}{n}\right) \cdots\left(1-\frac{k-1}{n}\right)-1\right] \frac{x^{k}}{k !} \rightarrow 0 \)
und folgern Sie, dass es ein \( n_{0} \in \mathbb{N} \) gibt, so dass für \( n \geq n_{0} \) gilt
\( \left|\left(1+\frac{x}{n}\right)^{n}-\sum \limits_{k=0}^{n} \frac{x^{k}}{k !}\right|<\varepsilon \)

Comments

Kannst du bitte sinnvollere Titel formulieren?

---

Wende den binomischen Satz auf (1+x/n)^n an, benutze die Definition der Binomialkoeffizienten, klammer aus jedem Summanden jeweils x^k/(k!) aus ....

Answer 1

Hallo Demet. Wir machen zunächst einfach, was in der Aufgabe steht:
Formelsammlung, „binomische Formel“:

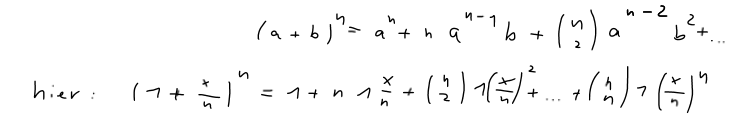
Formelsammlung, „Binomialkoeffizienten“:

Und jetzt? Wenn man sich die Rechnung mit z. B. n = 3 klar macht, kommt man auf Folgendes:
Zu zeigen ist:

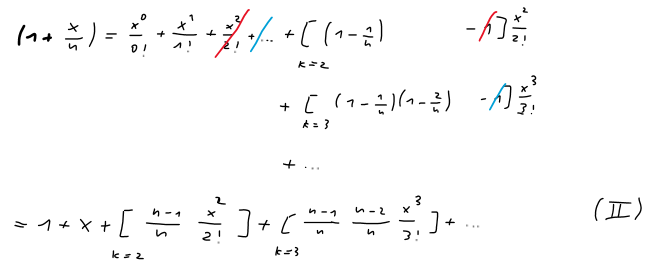
Da Term (I) = Term (II), ist die Gleichung bewiesen. Der Beweis muss nur noch schöner aufgeschrieben werden.

Comments

Noch eine Anmerkung: Der Startwert der zweiten Summe in

ist nicht 0, sondern 2.

---

Hallo Demet. Vielen Dank für "Beste Antwort".