Ableitung mithilfe der Kettenregel-Denkanstoß

Question

Aufgabe:

ich habe folgende Funktion von der ich die Ableitung mit Hilfe der Ketteregel bin und zwar

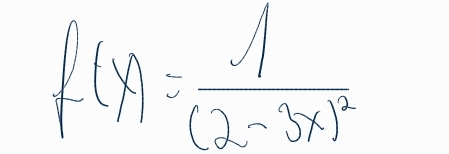
Da nur ein X im Nenner vokommt so kann man die Potenz im Nenner um eins erhöhen und ein negativ Vorzeichen schreiben

Nun muss man ja mithilfe der Kettenregel die Ableitung von (2-3x)^-2 bilden

Was ja -2(2-3x)^-3  -3--> 6 (2-3x)^-3  ergeben soll, aber Laut Wolfram kommt da 6 raus

Answer 1

Ja, 6 steht im Zähler, wenn man den negativen Exponenten beseitigt.

https://www.wolframalpha.com/input?i=derive+1%2F%282-3x%29%5E2

Answer 2

Du hast vermutlich bei wolframalpha falsch eingegeben. Die Exponenten musst Du mit dem Hütchen setzen, also (2-3x)^ {-2}, dann klappt's auch.

Und verschlanke mal Deine Merkregeln, man braucht hier nur \(x^n \longrightarrow n\cdot x^{n-1}\) mit \(n=-2\) (und die Kettenregel natürlich).

Answer 3

Aloha :)

Die innere Funktion habe ich mal pink markiert:$$f(x)=\frac{1}{(\pink{2-3x})^2}=(\pink{2-3x})^{-2}$$$$f'(x)=\underbrace{-2(\pink{2-3x})^{-3}}_{\text{äußere Abl.}}\cdot\underbrace{(\pink{-3})}_{\text{innere Abl.}}=\frac{6}{(2-3x)^3}$$

Deine Lösung ist also korrekt.

WolframAlpha meint das auch: https://www.wolframalpha.com/input?i=derive+1%2F%282-3x%29%5E2