Question

Berechnen Sie den Flächeninhalt der Fläche, die der Graph der Funktion \( f \) mit der \( x \)-Achse einschließt.

a) \( f(x)=4-x^{2} \)
c) \( f(x)=(x-2)(4-x) \)
b) \( f(x)=x(x-1)(3-x) \)
d) \( f(x)=-x^{2}+6 x+7 \)

Comments

Zur Kontrolle:

https://www.integralrechner.de/

---

Was ist Deine Frage zur Aufgabe?

Hier siehst Du die Funktionen (Reihenfolge der Farbgebung in der von Dir gewählten Nummerierung a, c, b, d: blau, gelb, grün, rot), deren Nullstellen und die gesuchten Flächen dazwischen:

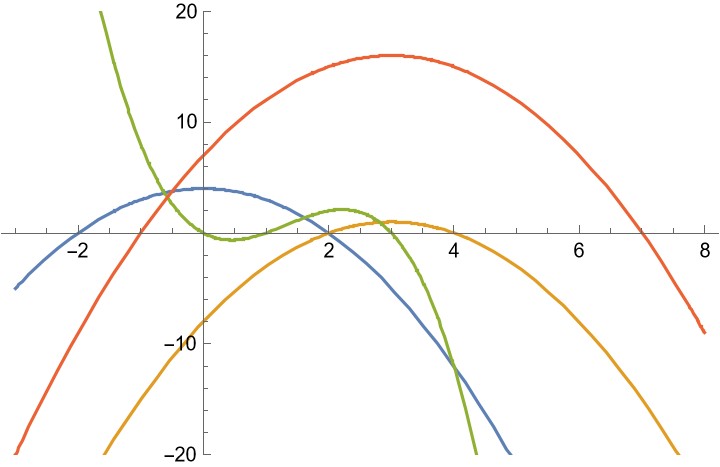
Bei der grünen Kurve wirst Du feststellen, dass der Flächeninhalt eine Summe ist. Denn es gibt drei Nullstellen anstatt zwei.

Answer 1

für a komme ich im Kopf auf 32/3. Es ist gut, dass dir das nicht weiterhilft.

Also, Nullpunkte bestimmen, grafisch anschauen und integrieren. Gerne bestätigen wir deine Ergebnisse und bei Unklarheiten bitte melden.

Answer 2

a) a) f(x)=4-x² hat die Nullstellen x₁= -2 und x₂ = 2 und es geht um die graue Fläche:

\( \int\limits_{-2}^{2} \)4-x²dx

Answer 3

a) \( f(x)=4-x^{2} \)     Nullstellen bei \(x_1=-2\)       \(x_2=2\)

Wegen der Achsensymmetrie:

\(\frac{A}{2}=\int\limits_{0}^{2}(4-x^{2})dx=[4x-\frac{x^3}{3}]_{0}^{2} =[4 \cdot 2-\frac{8}{3}]-[0]=\frac{16}{3} \)

\(A= \frac{32}{3} \)