Text erkannt:
Aufgabe 1
Bei einem medizinischen Test leert eine Versuchsperson ein Glas Wein in einem Zug.
Anschließend wird der zeitliche Verlauf der Blutalkoholkonzentration (in Promille) aufgezeichnet. Diese wird im hier verwendeten Modell zunächst durch eine Funktion \( f_{\mathrm{a}} \) mit der Gleichung
\( f_{\mathrm{a}}(t)=\frac{a}{60}\left(1-e^{-\frac{1}{20} t}\right)-\frac{1}{600} t \)
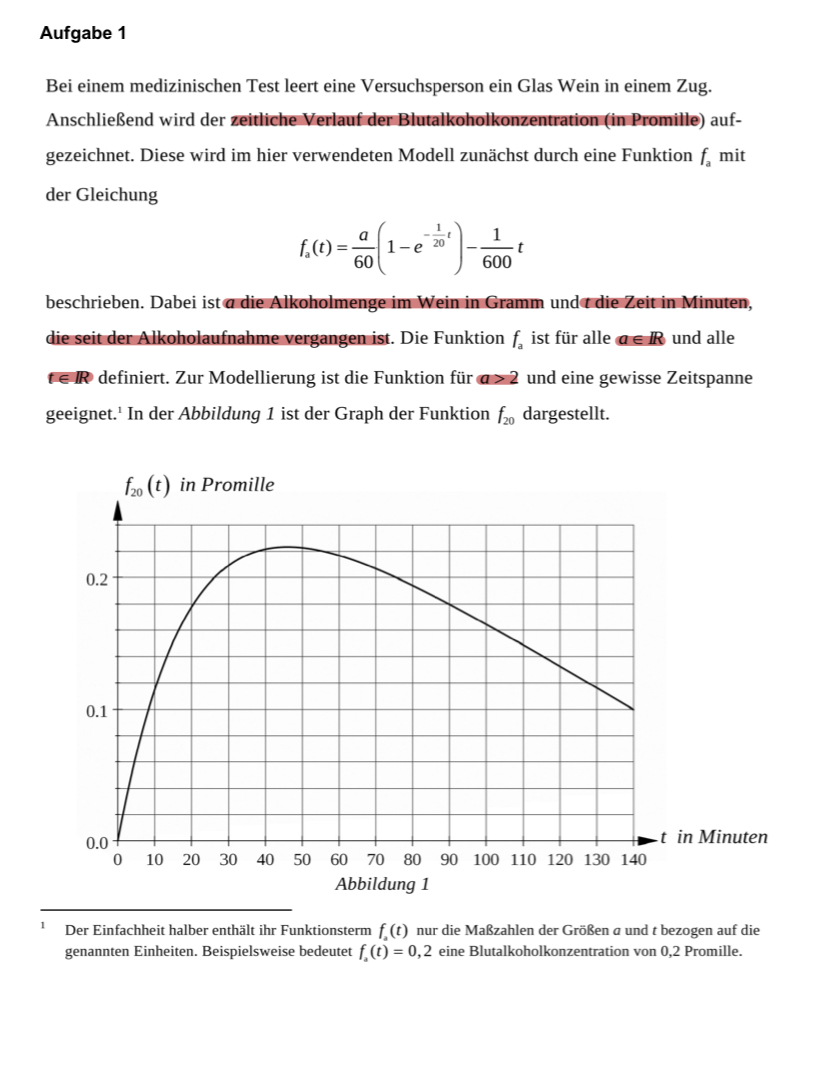
beschrieben. Dabei ist \( a \) die Alkoholmenge im Wein in Gramm und \( t \) die Zeit in Minuten, die seit der Alkoholaufnahme vergangen ist. Die Funktion \( f_{\mathrm{a}} \) ist für alle \( a \in \mathbb{R} \) und alle \( \boldsymbol{t} \in \mathbb{R} \) definiert. Zur Modellierung ist die Funktion für \( \boldsymbol{a}>2 \) und eine gewisse Zeitspanne geeignet. \( { }^{1} \) In der Abbildung 1 ist der Graph der Funktion \( f_{20} \) dargestellt.
1
Der Einfachheit halber enthält ihr Funktionsterm \( f_{a}(t) \) nur die Maßzahlen der Größen \( a \) und \( t \) bezogen auf die
genannten Einheiten. Beispielsweise bedeutet \( f_{a}(t)=0,2 \) eine Blutalkoholkonzentration von 0,2 Promille.

Text erkannt:
a) Bestimmen Sie die globale Maximalstelle \( t_{\mathrm{m}} \) der Funktion \( f_{a} \) in Abhängigkeit von \( a \). Begründen Sie den Einfluss des Parameters a auf die Lage der Maximalstelle und interpretieren Sie Ihre Ergebnisse im Sachzusammenhang.
[Zur Kontrolle: \( f_{\mathrm{a}}^{\prime}(t)=\frac{1}{600}\left(\frac{a}{2} e^{-\frac{1}{20} t}-1\right) ; t_{\mathrm{m}}=20 \ln \left(\frac{a}{2}\right) \) ]
Das Glas Wein, das die Versuchsperson in einem Zug leert, enthält 20 g reinen Alkohol. Die Blutalkoholkonzentration der Versuchsperson zur Zeit \( t \) nach dem Leeren des Glases wird nun für \( 0 \leq t \leq 140 \) durch die Funktion \( f \) mit der Gleichung
\( f(t)=f_{20}(t)=\frac{1}{3} \cdot\left(1-e^{-\frac{1}{20} t}\right)-\frac{1}{600} t \)
beschrieben.
b) (1) Berechnen Sie die höchste Blutalkoholkonzentration der Versuchsperson nach dem Leeren des Glases.
(2) Ermitteln Sie durch Integration eine Gleichung einer Stammfunktion \( F \) von \( f \).
[Zur Kontrolle: \( F(t)=\frac{1}{3}\left(20 e^{-\frac{1}{20} t}-\frac{1}{400} t^{2}+t\right) \) ]
(3) Berechnen Sie \( \frac{F(140)-F(0)}{140} \) und interpretieren Sie diesen Ausdruck im Sachzusammenhang.
(4) Berechnen Sie die Blutalkoholkonzentration der Versuchsperson 140 Minuten nach dem Leeren des Glases.
Ich benötige dringende Hilfe bei diese Aufgaben!