Sei f: U -> R eine Funktion, wobei U eine offene Teilmenge des R^n ist. Dann definiert man die Funktion g: I -> R, wobei I eine offene Teilmenge von R ist, als
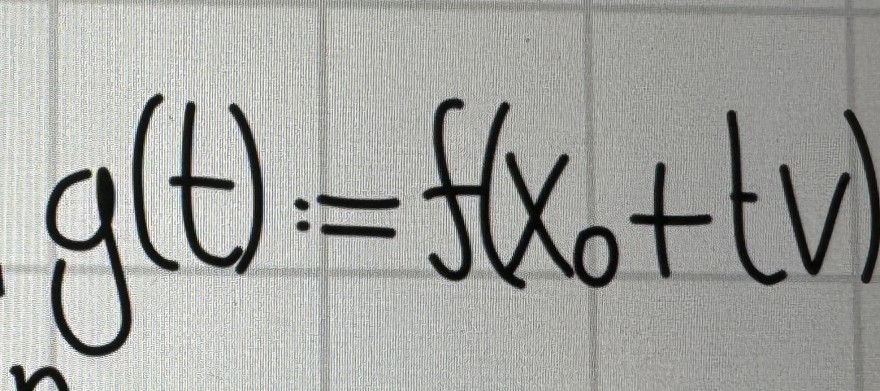
Text erkannt:
\( g(t)=f\left(x_{0}+t v\right. \)
Hierbei ist x0 aus U und v aus R^n.
Warum ist die erste Ableitung:

Text erkannt:
\( g^{\prime}(t)=\left\langle(\nabla f)\left(x_{0}+t v\right), v\right\rangle \)
Also ich hatte an die Richtungsableitungsdefinition gedacht, aber nach dieser müsste doch da beim Gradienten im Skalarprodukt das tv wegbleiben.