Hallo.
1) Zu deiner ersten Frage:
Beispiel: f(x,y) = 2x^2 + y^4. Das die Funktion für alle (x,y) partiell differenzierbar ist, sieht man ja, denn du kannst ohne Probleme die partiellen Ableitungen ausrechnen für beliebige (x,y). (Du hast also keine kritischen (x,y) hier)
In dem Falle sind die partiellen Ableitungen also die Funktionen f_x (x,y) = 4x und
f_y (x,y) = 4y^3. Das gilt für jedes (x,y).
————
Weiteres Beispiel:
f(x,y) = 1/(x+y) für (x,y) ≠ (0,0) und f(0,0) = 0
Hier siehst du, das für (x,y) ≠ (0,0) die Funktion wie oben mit den Ableitungsregeln partiell differenzierbar ist. Jedoch was ist mit dem Punkt (0,0)? Hier musst du also die hauptsächliche Definition nutzen, da du hier keine Ableitungsregel verwenden kannst.
Für die partielle Ableitung nach x im Punkt (0,0) ist der Grenzwert also:
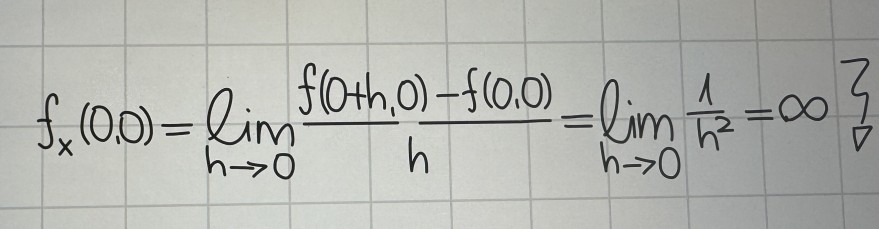
Text erkannt:
\( \left.f_{x}(0,0)=\lim \limits_{h \rightarrow 0} \frac{f(t h, 0)-f(0,0)}{h}=\lim \limits_{h \rightarrow 0} \frac{1}{h^{2}}=\infty\right\} \)
Also ist f nach x im Punkt (0,0) nicht partiell differenzierbar. Analog nach y.
Also auch insgesamt nicht in (0,0) partiell differenzierbar.
——-
Das heisst insgesamt kannst du die bekannten Ableitungsregel für beliebige (x,y) immer anwenden, jedoch kann es eben wie bei der zweiten Funktion auch mal einen Polpunkt (in dem Beispiel (0,0)) geben, wo du dann die hauptsächliche Definition nutzt. Es hängt also immer von der gegebenen Funktion ab. Meistens hast du solche Polpunkte eben bei anschnittsweise definierten Funktionen wie oben.
2) Zu deiner zweiten Frage:
Bei der Jacobimatrix ist nur die Existenz gefordert. Die zweite Bedingung deckt dann auch die Stetigkeit ab.