Die Methoden der Vektorrechnung ermöglichen es, Ergebnisse von Konstruktionen im Koordinatensystem rechnerisch nachzuvollziehen, sowie allgemein gültige Zusammenhänge herzuleiten.
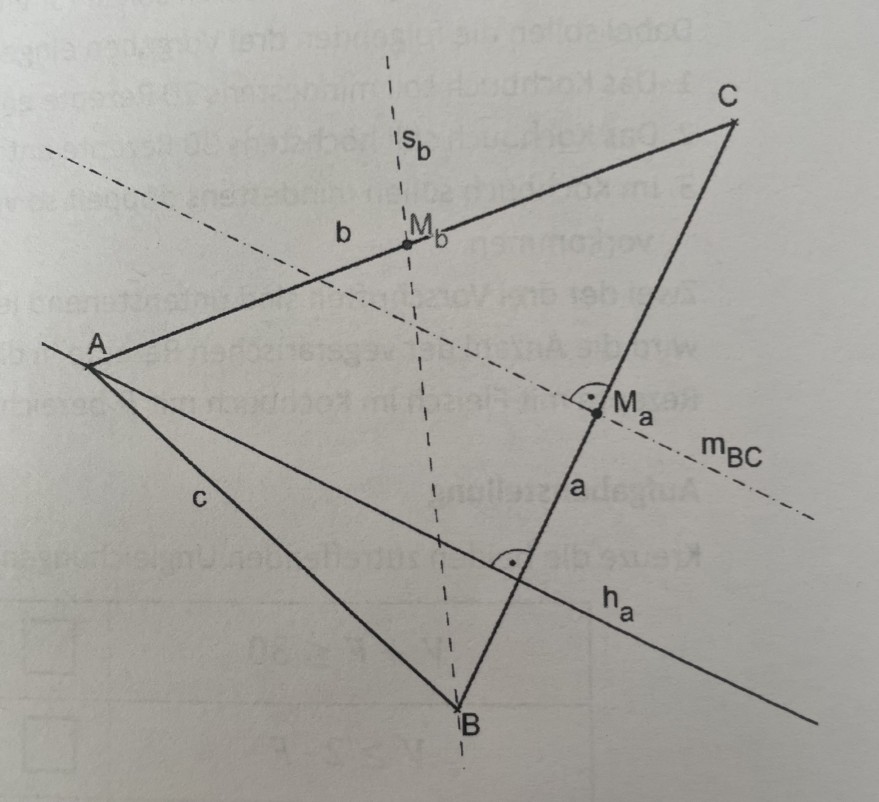
In der Abbildung sind zur Veranschaulichung die Schwerlinie \(s_b\) (strichliert), die Streckensymmetrale \(m_{BC}\) (punkt-strichliert) und die Höhe \(h_a\) eingezeichnet.
Gegeben ist das Dreieck $$ A = \begin{pmatrix} -2 \\ -3 \end{pmatrix},\: B = \begin{pmatrix} 7 \\ -5 \end{pmatrix},\: C = \begin{pmatrix} 4 \\ 7 \end{pmatrix}. $$
Aufgabenstellung:
a) Die Schwerlinien des Dreiecks verbinden jeweils den Mittelpunkt einer Seite mit dem gegenüberliegenden Eckpunkt. Der Mittelpunkt der Seite \(b\) hat die Koordinaten \({M_b = (1\vert 2)}\). Gib eine Gleichung der Schwerlinie \(s_b\) in Parameterform an und zeige, dass der Schwerpunkt \({S = \left(3\vert \frac{1}{3} \right)}\) auf der Schwerlinie liegt.
b) Stelle die Gleichung der Höhengeraden ha (siehe Skizze) auf die Seite a in Normalvektorform auf!
Ich weiß, nicht womit ich beginnen soll.
Lg Derrien