Das hier ist die aufgabe:
Text erkannt:
(17) Soit \( p \) un nombre premer. Mentrea que \( p \left\lvert\,\binom{ p}{k}\right. \) Matteo pour \( 1 \leqslant k \leqslant p-1 \).
(18) Soreat \( p \in \mathbb{P}, n \) un entios poritif, \( a, b \in \mathbb{Z} \). Montrer (paricurenen) Damis que \( p \mid\left((a+b)^{n}-\left(a^{n}+b^{n}\right)\right) \).
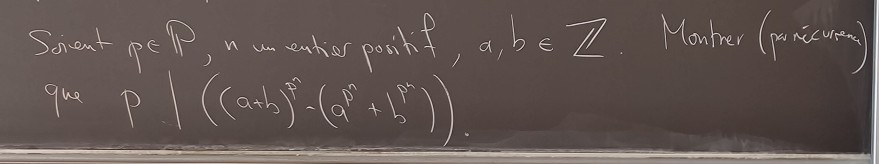
Text erkannt:
Sorient \( p \in \mathbb{P}, n \) un entios poritif, \( a, b \in \mathbb{Z} \). Montrer (parcécréneas) que \( P^{\mid} \mid\left((a+b)^{n}-\left(a^{p}+b^{n}\right)\right) \).