a) Handelt es sich bei dieser Funktion um die exponentielle Beschreibung eines Wachstums- oder eines Zerfallsprozesses? Begründen Sie ausschließlich anhand des Funktionsterms.
h(t) entspricht der Form h(t) = a·e^{k·t} mit k ≠ 0.
Für k > 0 liegt ein Wachstum und für k < 0 eine exponentielle Abnahme vor.
Hier hat man daher ein Wachstumsprozess.
b) Geben Sie den Wert für den Parameter a an, der der Aufgabenstellung entspricht.
a = 30000, wenn h(t) in m³ angegeben wird.
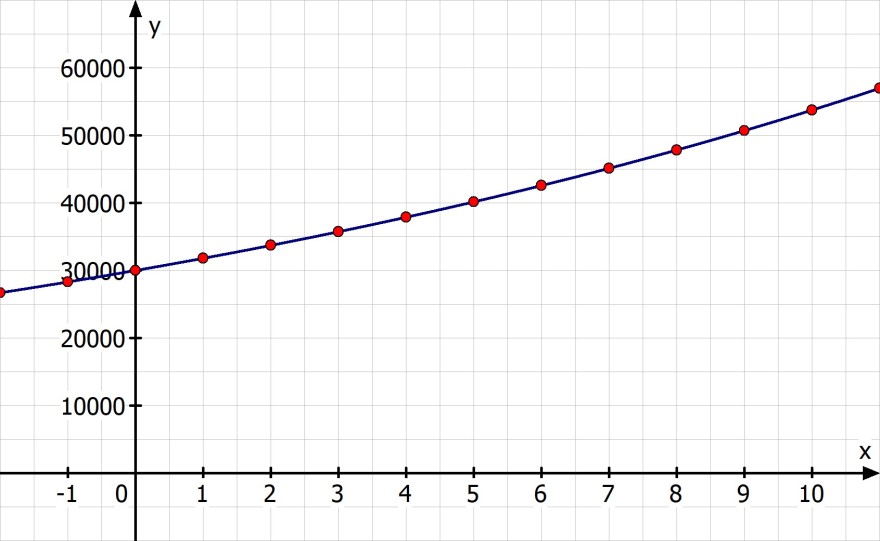
c) Erstellen Sie eine Wertetabelle, die jedem Jahr t den Holzbestand h(t) in m³ zuordnet. Wählen Sie 0 ≤ t ≤ 10 und stellen Sie den Zusammenhang in einem geeigneten Koordinatensystem dar.
[0, 30000;
1, 31801;
2, 33710;
3, 35734;
4, 37879;
5, 40153;
6, 42564;
7, 45119;
8, 47827;
9, 50699;
10, 53742]
d) Berechnen Sie den Funktionswert für t = -10. Interpretieren Sie das Ergebnis im Sachzusammenhang.
h(-10) = 16747 m³
Der Holzbestand betrug vor 10 Jahren etwa 16747 m³ wenn auch dort die Modellvoraussetzungen gegolten haben.