Es ist egal, ob man bei der Normalverteilung < oder ≤ benutzt. Genauso egal ist es ob du > oder ≥ benutzt. Ich benutze daher grundsätzlich ≤ und ≥.
a) kleiner als 100 cm ist?
P(X ≤ 100) = Φ((100 - 103)/4) = Φ(-0.75) = 0.2266
b) zwischen 98 cm und 108 cm liegt?
P(98 ≤ X ≤ 108) = Φ((108 - 103)/4) - Φ((98 - 103)/4) = Φ(1.25) - Φ(-1.25) = 0.8944 - 0.1056 = 0.7888
c) größer als 110 cm ist?
P(X ≥ 110) = 1 - P(X ≤ 110) = 1 - Φ((110 - 103)/4) = 1 - Φ(1.75) = 1 - 0.9599 = 0.0401
d) unter 93 oder über 113 cm liegt?
P(X ≤ 93 oder X ≥ 113) = 1 - P(93 ≤ X ≤ 113) = 1 - P(93 ≤ X ≤ 113) = 1 - (Φ((113 - 103)/4) - Φ((93 - 103)/4)) = 1 - (Φ(2.5) - Φ(-2.5)) = 1 - (0.9938 - 0.0062) = 0.0124
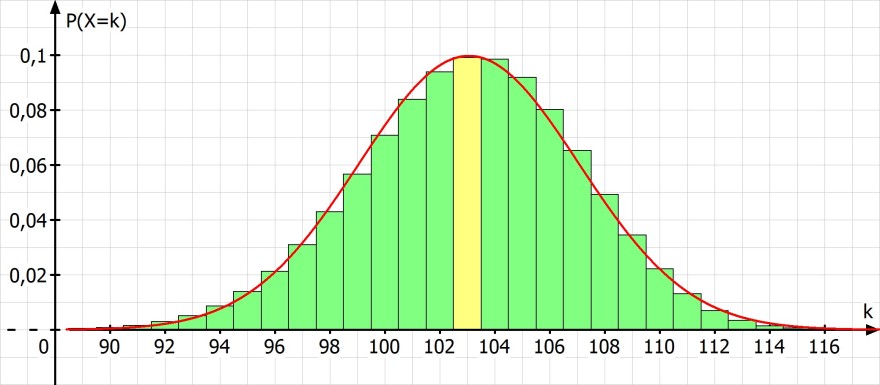
Folgend ist die stetige Normalverteilung und eine näherungsweise passende Binomialverteilung auszugsweise gezeichnet.