Hi,
setze zunächst mal f(x)=g(x), also beide Funktionen gleich setzen und deren Schnittpunkte bzw. Intervallgrenzen berechnen ;)
x2=2-x2
-2x2+2=0
x1=1
x2= -1
Das sind deine Schnittpunkte bzw. deine Intervallgrenzen. Jetzt bildest Du die Stammfunktion ;)
$$ \int_{-1}^{1}-2x^2+2dx=[-\frac { 2 }{ 3 }x^3+2x]{ }_{ -1 }^1=\frac { 4 }{ 3 }-(-\frac { 4 }{ 3 })=\frac { 8 }{ 3 }FE $$
Also beträgt die Fläche zwischen den beiden Funktione 8/3 FE
Hier der Graph:
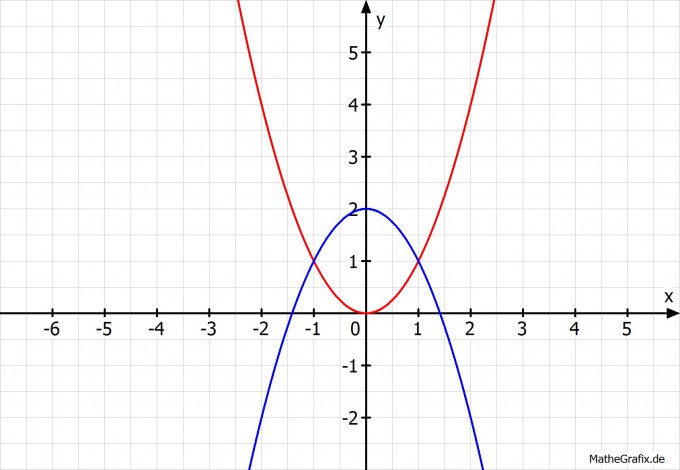
Gruß