K ist das Schaubild der Funktion f(x)=(2/3)x2 +(1/3)x+1
a) K und die Gerade y=2x+1 begrenzen ein Flächenstück.
Dieses Flächenstück rotiert um die x-Achse und erzeugt einen Drehkörper.
Berechnen Sie das Volumen des Drehkörpers.
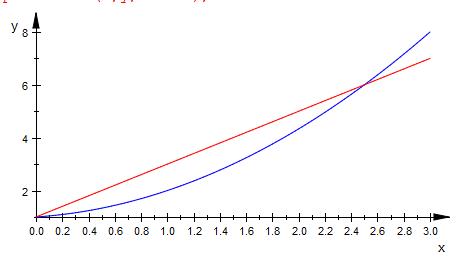
Es dürfte sich um den Bereich zwischen der blauen Kurve ( f ) und
der roten Kurve ( y ) handeln.
Schnittpunkte : x = 0 und x = 2.5
Das Volumen der roten Kurve
y ( x ) = 2 * x + 1
Ay ( x ) = y^2 * π
Ay ( x ) = ( 2 * x + 1 )^2 * π
Ay ( x ) = ( 4 * x^2 + 6 * x + 1 ) * π
Stammfunktion
∫ Ay ( x ) * dx
π ∫ 4 * x^2 + 6 * x + 1 dx
π [ 4 * x^3 / 3 + 6 * x^2 / 2 + x ]
Volumen
π [ 4 * x^3 / 3 + 6 * x^2 / 2 + x ]02.5
V(ay) = 112.57
Dasselbe mit f ( x ) auch durchführen.
Dann V(f) von V(ay) abziehen.
Bin bei Bedarf gern weiter behilflich.