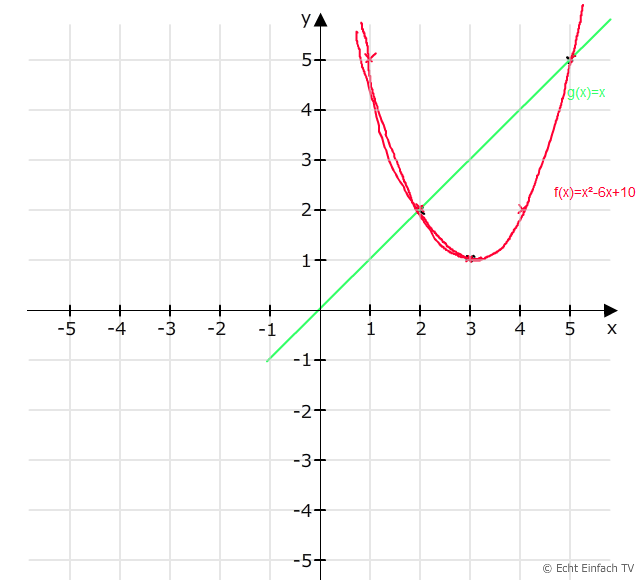
aus den Funktionen kan man bereits einiges "ablesen"
die erste ist eine Parabel nach oben geöffnet da vor dem x² ein + steht, also positiv ist , und eine quadratische Funktion mit einem Schnittpunkt der y Achse bei +10
die Zweite ist eine Linearfunktion mit dem Ursprung (0/0)
wenn man f(x)=x²-6x+10 in eine Scheitelpunktform bringt erhält man
f(x) =(x-3)²+1 der Scheitelpunkt liegt also bei S(3/1)
Funktion f(x) liegt also Quadranten 1+4 und g(x) im Quadranten 1+3
Für die Schnittpunkt setzt man beide Funktionen gleich
f(x)=g(x)
x²-6x+10=x |-x
x²-7x+10=0 |pq-Formel anwenden
x1,2=(7/2)±√(49/4)-10
x1,2=(7/2)±(3/2) ⇒x1=5 x2=2 Die Schnittpunkte der beiden Funktionen liegen bei P(5/5) und Q(2/2)
Probe:f(2)=4-12+10=2 f(5)=25-30+10=5
siehe Skizze