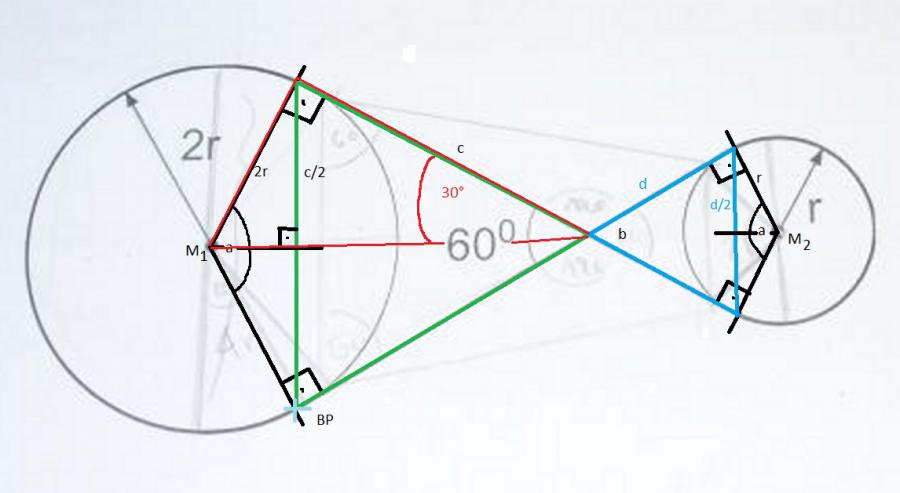
Berechnung von l in Abhängigkeit von r:
Der Riemen bildet zusammen mit dem Radius ein großes und ein kleines Drachen-Viereck.
(Der Riemen ist ja wie eine Tangente an den Kreis. Wenn man also eine Strecke von den Berührpunkten BP (einer beispielhaft eingezeichnet) des Riemens außen am Kreis zum Mittelpunkt M1 und M2 der Kreise zeichnet erhält man die Drachen-Vierecke.)
Die Strecke Kreismittelpunkt - Berührpunkt steht senkrecht auf dem Riemen. Man kennt also den Winkel --> 90°.
Winkelsumme im Viereck 360°:
a = 360° -90° -90° -60° = 120°;
Grünes Dreieck ist gleichseitig:
(c/2) / (2*r) = sin(60°) --> c = 4*r*sin(60°) = 2*sqrt(3)*r
Blaues Dreieck ist gleichseitig:
(d/2) / r = sin(60°) --> d = sqrt(3)*r;
Teilumfang großer Kreis:
phi = 360° -120° = 240° = 4/3*pi;
Ug = phi*2*r = 8/3*pi*r;
Teilumfang kleiner Kreis:
phi = 4/3*pi;
Uk = phi*r = 4/3*pi*r;
Länge des Riemens:
l = Ug +Uk +2*c +2*d =
= 8/3*pi*r +4/3*pi*r +4*sqrt(3)*r +2sqrt(3)*r =
= r* [ 2* (2*pi +3*sqrt(3) ) ];
Für l = 5m ist r:
r = l / [ 2*(2*pi +3*sqrt(3)) ] = 5m / [ 2*(2*pi +3*sqrt(3)) ] = 0,22 m;
lg JR
Ergänzung:
Ich habe noch das rote rechtwinklige Dreieck gekennzeichnet. Das kannst Du auch verwenden um c zu berechnen, so wie es Mathecoach gemacht hat. Das ist meiner Meinung nach auch die bessere Lösung. Meine funktioniert nur weil der Winkel beim Riemen gerade 60° ist.