Pyramidenstumpf Volumen

Question

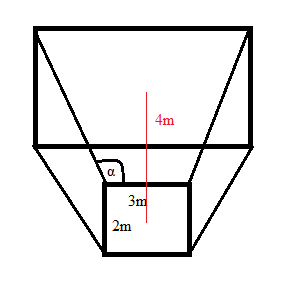
ein Freund hat mir dieses Forum empfohlen, weil ich gerade wirklich nicht weiterkomme. Es geht um Pyramidenstümpfe. Speziell im Baubereich - Erdaushübe. Heißt der Pyramidenstumpf ist auf den Kopf gestellt.

Meine Aufgabe ist: Erstelle eine Excel-Datei, in der die Kollegen nur noch das eintragen müssen, was gerade gegeben ist und ihnen dann das Volumen ausspuckt.

Gegeben könnte demnach sein Länge 2 und Breite 2, Höhe und α, wobei α je nach Boden eigentlich nur 30°, 45° oder 60° sein kann. Aushübe sind entweder quadratisch oder rechteckig.

Soweit so gut. Mein letzter Mathematikunterricht ist 9 Jahre her. Geometrie und Trigonometrie waren nicht unbedingt meine Stärken und in den letzten Jahren habe ich nicht mal einen einfachen Würfel berechnen müssen.

Ich bräuchte Hilfe beim Verstehen und beim Erarbeiten (vielleicht sogar der Formel, wenn sich hier auch jemand im Excel auskennt?) der Rechnung. Mein Chef - von dem der Auftrag kam - hat es so erklärt, als hätte ich selbst Bauingenieurwesen studiert. Mitgekommen bin ich schon, aber umsetzen... keine Chance. Vielleicht mache ich es mir auch umständlich...

Ich müsste schrittweise wissen, wie ich an das Volumen komme, wenn ich die Länge und Breite der Schnittfläche, sowie die Höhe und den Winkel des Aushubs, also des Trapez habe.

Wir können ja als Beispiel sagen, dass man 2 x 3 Meter in 30° 4 Meter hoch ausgräbt.

Ich hoffe hier kann mir jemand helfen... ich hab sicherlich schon einen kompletten Arbeitstag dafür verwandt und zig Seiten gelesen, aber es hat einfach noch nicht klick gemacht :-(

Comments

Wo wird der Winkel Alpha genau gemessen ? Der ist in Deiner Skizze ja dann schon verkehrt oder nicht ?

---

Bei dir ist alpha ein stumpfer Winkel, das ist doch wohl

nicht gemeint sondern eher oben an der Baugrupe gemessen.

Was bedeutet dann 30°  ?

ist das eher steil oder flach, also senkrecht runter wäre 0° oder 90° ?

---

Das Ding in Excel zu programmieren ist kein Problem. Aber die Angaben müssen klar sein. Also z.b. wo der Winkel gemessen wird. In deiner Skizze ist er größer als 90°. Das passt also nicht zu deinem Text.

---

Ähm... der Winkel ist der Winkel, den man sozusagen gräbt. 90 ° wären vertikal nach oben, wie bei einem Würfel und je nach Boden gräbt man im Grunde flacher... Ich habs mal versucht es nochmal zu zeichnen und entschuldige mich gleich für die unqualifizierte Antwort:

30° wäre sehr flach gegraben (z. B. Sand, welcher sonst einfach "nachfließen" würde

45° wäre schon ein steilerer Hang

60° wäre noch steiler

Vielleicht hilfts zum Verstehen, dass man steiler graben kann, je stabiler und fester das Bodenmaterial.

Hilft das?

Answer 1

Ich nehme mal an der Winkel α ist der Tiefenwinkel einer Seite

Neigungswinkel der Seitenfläche α

tan(α) = h/x --> x = h/tan(α)

Untere Fläche A1

A1 = a·b

Obere Fläche A2

A2 = (a + 2·x)·(b + 2·x)

Volumen des Aushubs

V = 4/3·h·x^2 + x·(a·h + b·h) + a·b·h

Comments

Coach, müsste man bei A2 das x nicht zweimal nehmen?

---

Und wenn a und b nicht gleich sind, müsste man dann nicht klären wo der Winkel gemessen wird. Denn die Tiefenwinkel dürften nicht gleich sein, wenn a und b unterschiedlich sind.

---

Ja du hast recht. Das x sollte 2 mal genommen werden. Ich habe das verbessert.

Aber der Tiefenwinkel sollte mal an jeder Seite gleich sein. Hat doch wohl damit zu tun das bei zu steilen Aushüben die Bodenschichten wegbrechen würden.

---

Coach, wie soll das gehen? Ein pyramidenstumpf mit rechteckiger Grundfläche hat doch an der Grundfläche (also der größeren) nicht die gleichen Winkel. Das wäre aus meiner Sicht nur bei der quadratischen Variante gegeben.

---

Ich denke es handelt sich hier nicht wirklich um einen Pyramidenstumpf. Das wäre nur bei quadratischer Grundfläche so.

Der Winkel ist ja baubedingt. Stell dir eine Sanduhr vor. Dort entsteht ein Schüttkegel. Der Neigungswinkel der Seitenlinie kann einen bestimmten Wert nicht übersteigen. Da sonst Sand von oben nachrutschen würde.

Wenn ich also in meinem Garten eine Schwimmbahn ausheben möchte. 25 m lang und 1 m breit. Dann wird das sicher kein Pyramidenstumpf werden.

Ich denke das hat man hier nur so bezeichnet weil es dem am nächsten kommt und man sich vorstellen kann was damit gemeint ist.

Oder weißt du einen anderen Ausdruck für den entstehenden Körper ?

---

Oh Schitt. Dann kann ich natürlich auch nicht mit der Formel für einen Pyramidenstumpf rechnen ...

---

Mathecoach liegt ganz richtig. Also was das mit dem Sand angeht. Man sagt wohl, dass man bei Sand ca. 30° nimmt, also sehr flach aushebt und bei stabilerem Untergrund wie fester Erde 60° nehmen kann. Kies wäre glaube ich 45°. Eben anhand dem, was nachrutschen könnte.

Im Grunde geht es darum, dass man einen Fundamentblock in die Erde packt und dafür den Aushub vornehmen muss. Und diesen Aushub - also das Volumen - brauchen wir zum Kalkulieren.

Mein Chef weiß an sich schon, wie sie es bisher berechnet haben... aber er konnte mir das nicht wirklich schlüssig erklären und schon gar nicht so, dass ich es im Excel umsetzen kann. Formeln und sowas sind für mich zwar kein Problem, aber ich muss dazu verstehen, was ich eigentlich mache. Und daran scheitert es im Moment leider.

---

Schau dir mal meine obigen nachgebesserten Formeln an. Mache damit erstmal eine Excel Tabelle. Das sollte nicht schwer sein. Du hast ja immer nur 4 Werte.

Dann überprüfst du die Werte mit alten vom Chef berechneten werten. Dann hast du eine gute Kontrolle.

Answer 2

Legen Sie sich sowohl für jede gegebene Größe eine Spalte an (A,B,C,D,E) als auch verscheide Teilterme (F,G,H,I,J). Und dann noch eine Spalte K für den Gesamtterm. Beispiel: Angenomme Sie arbeiten mit der Formel V=h/3(G+S+√(G·S). Dabei ist G=a·b die Grundfläche und S=c·d die Deckfläche des Pyramidenstumfes mit der Höhe h. Dann brauchen Sie eine Tabelle mit 11 Spalten
A  B  C  D  E      F           G         H       I           J              K

a  b  c   d   h  G=a·b  S=c·d  √(G·S) h/3 G+S+√(G·S)  I1·J1