Wie bestimme ich mit einer Verknüpfungstabelle die Nullteiler, hier Z9?

Question

Ich suche im Körper (Z9,+,*) Nullteiler mit der Verknüpfungstabelle.

Meine erste Frage: In welcher Verk,nüpfungstabelle stehen die eigentlich?

Zweite Frage: Wie finde ich die in der Tabelle?

Answer 1

Guten Morgen Mathemagiker,

kennst Du die Definition eines Nullteilers? Der Nullteiler eines Rings, in Deinem Fall $$(\mathbb{Z}/9\mathbb{Z},+,\cdot),$$ ist ein Element $$a\neq0$$ für das es ein vom Nullelement (0) verschiedenes b mit $$a\cdot b=0$$ gibt. Aus dieser Definition kannst Du bereits ablesen, dass Nullteiler in der Verknüpfungstabelle der Multiplikation zu suchen sind, da sich diese Eigenschaft auf das Produkt bezieht. Betrachten wir nun die besagte Verknüpfungstabelle:

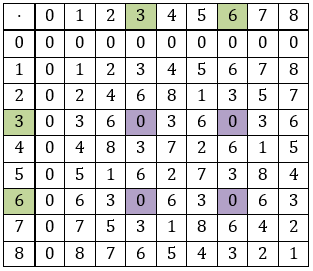
1. Du suchst nach allen Nullen in der Tabelle (die Nullen, die durch die Nullen an den Tabellenrändern entstehen, werden vernachlässigt, da a und b ungleich 0 nach der Nullteilerdefinition sind). In der obigen Tabelle sind diese lila markiert.

2. An den entsprechenden Tabellenrändern stehen nun die Nullteiler. Diese habe ich hier grün gekennzeichnet.

Als Ergebnis kannst Du also festhalten: Im Ring $$(\mathbb{Z}/9\mathbb{Z},+,\cdot)$$ gibt es die Nullteiler 3 und 6.

Ich antworte gerne auf Rückfragen, falls noch etwas unklar sein sollte.

André, savest8