Mathemagiker,
Deine Formel für die n-te Ableitung ist richtig. Beim Induktionsschritt nutzt Du aus, dass die (n+1)-te Ableitung die Ableitung der n-ten Ableitung ist. Das ist bei Induktionsbeweisen von Ableitungsfunktionen ein gängiges Prozedere. Du erhältst also: 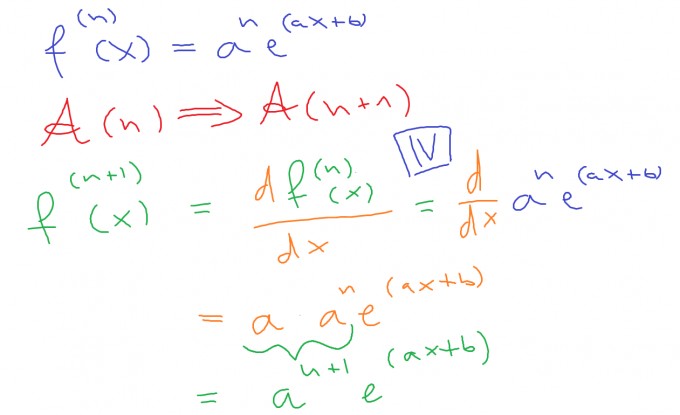
Damit ist die Behauptung bewiesen.
Hilft Dir das weiter? Wenn Du etwas nicht verstehen solltest, dann zögere nicht nachzufragen!
André, savest8