Konstruktion eines Dreiecks aus den Abständen eines inneren Punktes von den Ecken

Question

Gegeben ist ein innerer Punkt P eines gleichseitigen Dreiecks ABC sowie seine Abstände PA, PB und PC von den Ecken. Wie kostruiert man jetzt das Dreieck?

Answer 1

Zeichne den Punkt $P$ und trage daran beginnend die Strecke PA ab. Das Ende dieser Strecke sei $A$. Schlage nun um $A$ und $P$ (falls nicht schon geschehen) jeweils einen Kreis mit dem Radius PA (rot). Die Kreise schneiden sich in $Q$. Dann noch einen Kreis um $P$ mit dem Radius PB (blau) und einen weiteren Kreis $k$ mit dem Radius PC (grün).

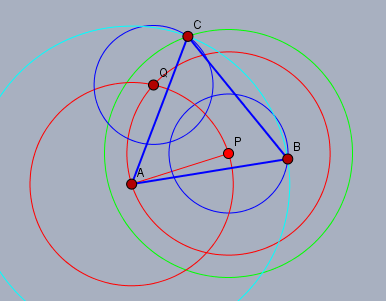
Ein Kreis um $Q$ mit dem Radius PB schneidet den Kreis $k$ (grün) um $P$ in $C$. Ein Kreis um $A$ mit dem Radius AC schneidet den Kreis um $P$ mit dem Radius PB in $B$ - man wähle den Schnittpunkt, bei dem der Winkel BAC unter $60°$ erscheint.
Bem.: Es existiert noch eine zweite Lösung, da der Kreis um $Q$ den grünen Kreis noch in $C\prime$ schneidet. Aber da liegt $P$ dann außerhalb des Dreiecks.

Comments

Danke für den Lösungsvorschlag, dessen Lesbarkeit noch gesteigert werden könnte durch Festlegungen wie K_P(PA)= Kreis um P mit dem Radius PA und dann K_P(PA)∩K_A(PA)=Q und in diesem Sinne weiter. Wenn du das noch anfügst, prüfe ich die Konstruktion auf Richtigkeit.

---

Die Konstrution ist richtig. (ein bisschen umständlich in der Beschreibung und in der Durchführung)

---

Hallo Roland,

Dein Ansinnen die 'Lesbarkeit' in der von Dir vorgeschlagen Weise zu steigern erstaunt mich. Als ich gelernt habe, wie man Konstruktionsbeschreibungen erstellt, habe ich das in der von mir oben gezeigten Weise gelernt. Ist schon 'ne Weile her. Der betreffende Lehrer wäre nie auf die Idee das Zeichen $\cap$ im Kontext mit geometrischen Symbolen zu benutzen. Was nicht heißen soll, dass ich das heute anders sehe. Zum Thema Mengenlehre meinte er damals sinngemäß: "Von Mengenlehre halte ich nichts. Müssen wir aber machen, weil es im Lehrplan steht" ;-)

Nun ja. man lernt nie aus. Ich will's mal versuchen:

Zeichne die Strecke $PA$.

$Q = \{ K_P(PA) \cap K_A(PA)| \omega PAQ = \frac{\pi}{3} \}$ $C = \{ K_Q(PB) \cap K_P(PC)| \omega PQC \le \pi \}$ $B = \{ K_P(PB) \cap K_A(AC)| \omega PAC=\frac{\pi}{3} \}$

Bem.: für das Winkelsymbol habe ich den LaTeX-Ausdruck nicht gefunden $\omega$ soll  sein!

Gruß Werner

---

Hallo Werner, vielen Dank, dass du dir die Mühe gemacht hast, die vom mir vorgeschlagene Stenographie einer Konstruktionsbeschreibung nachzuliefern. Ich finde das so tatsächluch besser lesbar. Für mich erwächst Mathematik auch aus dem Bemühen, immer mehr immer übersichtlicher auszudrücken.

Aus der Tatsache, dass dein Lehrer noch mit der Mengenlehre haderte, schließe ich auf dein Alter von 60+. Ich kann die Haltung deines Lehrers zur Mengenlehre gut verstehen. Von ihm wurde etwas verlangt, ohne ihn darauf vorzubereiten. Das kommt gerade in der Mathematik-Didaktik häufiger vor.