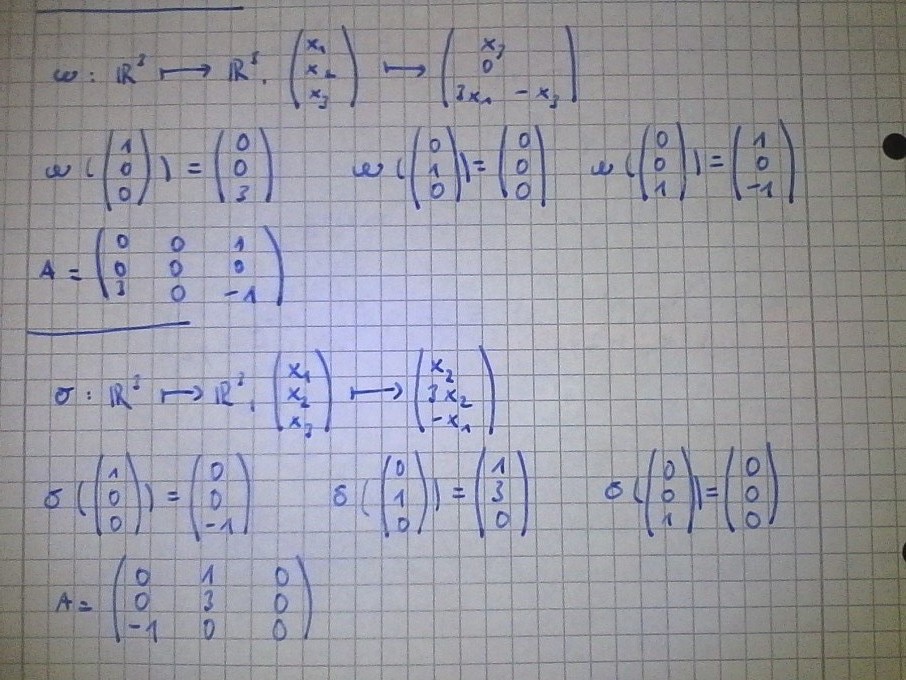komposition zweier matrizen, lineare abbildungen

Question

Ich habe versucht diese Aufgabe zu lösen, bin mir aber nicht so sicher ob es richtig ist..

Seien die folgenden linearen Abbildungen gegeben:
$$\begin{array}{l} {\omega: \mathbb{R}^{3} \mapsto \mathbb{R}^{3},\left(\begin{array}{l} {x_{1}} \\ {x_{2}} \\ {x_{3}} \end{array}\right) \mapsto\left(\begin{array}{c} {x_{3}} \\ {0} \\ {3 x_{1}-x_{3}} \end{array}\right)} \\ {\sigma: \mathbb{R}^{3} \mapsto \mathbb{R}^{3},\left(\begin{array}{l} {x_{1}} \\ {x_{2}} \\ {x_{3}} \end{array}\right) \mapsto\left(\begin{array}{c} {x_{2}} \\ {3 x_{2}} \\ {-x_{1}} \end{array}\right)} \end{array}$$
Bestimme jeweils die Matrizen der Abbildungen und dann mit (S $\nearrow 14.6,$ Bemerkung danach) und $(S \nearrow 14.8)$ die Matrizen von $(\omega+\sigma)(v),(5 \cdot \sigma)(v)$ und $(\omega \circ \sigma)(v)$

Hier meine Lösungen:

Answer 1

Hallo maben,

ich kann in deiner Lösung keinen Fehler entdecken :-)

Gruß Wolfgang

Comments

Wow! Das habe ich echt nicht erwartet, danke! :D