Folge auf Konvergenz untersuchen und Grenzwert angeben

Question

Hi zusammen,

hier ist eine Folge, die auf Konvergenz untersucht werden muss. Wenn vorhanden, soll man einen Grenzwert angeben:

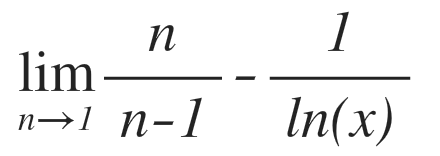
Ich habe schon diverses versucht. Durch Umformung in allen erdenklichen Formen bis alles Seitenlang wurde und durch l'hospital.

L'hospital habe ich als Notlösung versucht, da es nicht gezeigt wurde und somit fragwürdig ist, ob es akzeptiert wird.

Könnt ihr mir einen Ansatz geben, womit ich weiter arbeiten kann?

EDIT: Vielleicht sollte ich noch sagen, dass l'hospital auch nach der 2. Ableitung immer noch 0/0 liefert. Das habe ich natürlich erst gemacht, als ich die Brüche auf den gleichen Nenner gebracht habe.

Also:

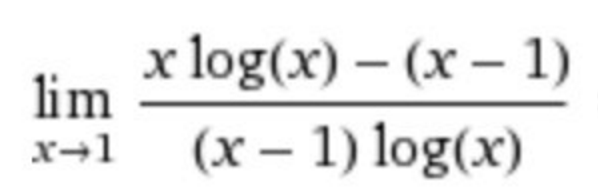
Im Übrigen liefert Wolfram Alpha als Ergebnis 1/2. 

Answer 1

Hallo wolfi,

 lim_x→1 [ (x·LN(x) - (x - 1)) / ((x - 1)·LN(x)) ]   =   lim_x→1 [ Z(x) / N(x) ]

nach 2-mal Hospital hast du wegen 

Z'(x)  =  [ x·LN(x) - (x - 1) ] ' =  ln(x)  und  N'(x) =  [ (x - 1)·LN(x) ] ' =  LN(x) + (x - 1)/x

 lim_x→1 [ Z'(x) / N'(x) ]  = " 0/0 " 

Z"(x)  =  [ x·LN(x) - (x - 1) ] "  = 1/x      und   N"(x)  =  [ (x - 1)·LN(x) ] "   =  1/x + 1/x² 

lim_x→1   \(\frac{1/x}{1/x+1/x^2}\)  = \(\frac{1}{2}\) 

Gruß Wolfgang

 

Comments

OMG und ich dachte ich bin aufgeschmissen. Danke :)

---

Hab es nochmal verschriftlicht. Anscheinend hatte ich mich vorhin verrechnet.
Aber noch eine andere Frage. Gibt es eine Möglichkeit ohne l'hospital die dir in den Sinn kommt? Würde damit dann rumprobieren.

---

Da fällt mir leider auch nichts ein.

Dein 2. "Rahmenterm", von dem ich ausgegangen bin, macht übrigens nur Sinn, wenn du im 1. RT  x für n schreibst.  Das wäre dann kein Folgen- sondern ein Funktionsterm.

So wie der 1. RT dasteht, ergibt er sowieso keinen Sinn.

---

so sollte es auch sein. Danke :)