Zeichnen Sie die Pyramide und bestimmen Sie das Volumen der Pyramide.

Question

Aufgabe:

Der Koordinatenursprung $\mathrm{O}$ und die Punkte $\mathrm{A}(7 | 3 | 0)$ und $\mathrm{B}(0|3| 0)$ sind Ecken der Grundfläche einer dreiseitigen Pyramide. Der Punkt $S(0|0| 7)$ ist die Spitze der Pyramide.

Zeichnen Sie die Pyramide und bestimmen Sie das Volumen der Pyramide.

Answer 1

Die Höhe kannst du an der z-Koordinate von S ablesen.

Also h = 7   Längeneinheiten.

Die Grundfläche ist ein halbes Rechteck. Daher kannst du G einfach ausrechnen. Zeichne den Grundriss in ein xy-Koordinatensystem ein, damit du erklären kannst, was du da machst.

Die Formel für das Volumen findest du hier: https://de.wikipedia.org/wiki/Pyramide_(Geometrie)#Formel

$V=\frac{1}{3} \cdot G \cdot h$

https://www.matheretter.de/geoservant/de?draw=vektor(0%7C0%7C0%200%7…

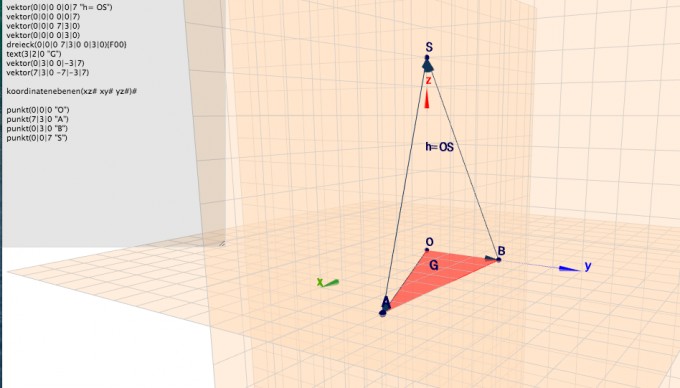
Im obigen Link ist dieses Bild beweglich zu sehen. Im Eingabefeld steht:

vektor(0|0|0 0|0|7 "h= OS")
vektor(0|0|0 0|0|7)
vektor(0|0|0 7|3|0)
vektor(0|0|0 0|3|0)
dreieck(0|0|0 7|3|0 0|3|0){F00}
text(3|2|0 "G")
vektor(0|3|0 0|-3|7)
vektor(7|3|0 -7|-3|7)
koordinatenebenen(xz# xy# yz#)#

Leider ist ausgerechnet h= OS nur sehr schwach eingezeichnet und der rote Pfeil, der die z-Achse markiert irritiert, weil er zu weit unten ist.

Answer 2

Ich füge nochmal eine etwas einfachere Volumenberechnung an.

OA = A = [7, 3, 0]

OB = B = [0, 3, 0]

OS = S = [0, 0, 7]

V = 1/6·([7, 3, 0] ⨯ [0, 3, 0])·[0, 0, 7] = 24.5

Wenn dieses im Unterricht nicht so gemacht werden soll, so ist dieses sehr gut geeignet um die eigenen Ergebnisse zu prüfen.

https://www.matheretter.de/rechner/schragbild?draw=dreieck(0%7C0%7C0…

Comments

In den lösungen meines mathebuches ist das Volumen 73,5

---

Ich würde fast sagen da irrt sich die Lösung. 73. 5 wäre das Volumen eines Dreiecksprismas mit der Grundfläche und einer Höhe von 7.