Hallo.
Es wäre nett, wenn mir jemand bei folgender Aufgabe helfen könnte. Mir geht es darum
Es sollen folgende Aussagen mithilfe der Definition der Mengengleichheit bewiesen werden.
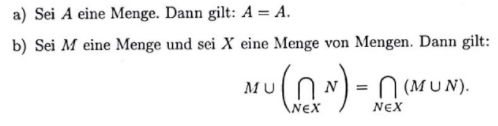
Definition der Mengengleichheit
1. Definition
A = B ⇔ ∀x (x ∈ A ⇔ x ∈ B)
2. Definition
A=B⇔A⊆B∧B⊆A
Schreibe ich also bei a) einfach nur hin
a) ∀x (x ∈ A ⇔ x ∈ A)
Wie ist das bei b) wie schreibt man das am besten auf?