Hallo Jibl,
Du schriebst: "Könnten sie mir auch die andere frage die ich gestellt habe so Präzise erklären ... "
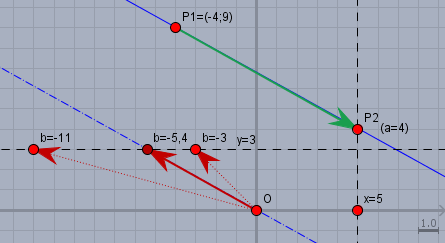
Wen es um Funktionen und noch mehr mehr, wenn es um Vektoren geht, so mache Dir IMMER eine Skizze. Ich habe zunächst mal die gegebene Gerade \(g_1\) (blaue durchgezogene Linie) mit dem Aufpunkt \(P_1=(-4;9)^T\) und dem Richtungsvektor \((9;-5)\) (grüner Pfeil) eingezeichnet.
Jetzt soll eine Geradengleichung für \(g_2\) gefunden werden, so dass \(g_2=g_1\) ist. Mit der Bedingung
$$g_2: \space r(\mu) = p_2 + \mu \cdot d_2 = \begin{pmatrix} 5\\ a\end{pmatrix} + \mu \begin{pmatrix} b\\ 3\end{pmatrix}$$
Damit \(g_2 = g_1\) ist, muss der Punkt \(P_2\) auf \(g_1\) liegen. Dazu habe ich die senkrechte gestrichelte Linie \(x=5\) eingezeichnet. Dort soll \(P_2\) liegen, da seine X-Koordinate \(=5\) sein soll. Ebenso muss er auf \(g_1\) liegen - also kommt nur der Schnittpunkt in Frage und der liegt in diesem Fall genau am Ende des Richtungsvektors von \(g_1\). Folglich ist
$$p_2 = p_1 + 1 \cdot d_1 = \begin{pmatrix} -4\\ 9\end{pmatrix} + \begin{pmatrix} 9\\ -5\end{pmatrix} = \begin{pmatrix} 5\\ 4\end{pmatrix}= \begin{pmatrix} 5\\ a\end{pmatrix} $$
\(a\) muss also \(a=4\) sein. Rechnerisch sieht das so aus, dass man den gegebenen Punkt \(P_2=(5;a)^T\) in die Gleichung für \(g_1\) einsetzt:
$$ \begin{pmatrix} 5\\ a\end{pmatrix} = \begin{pmatrix} -4\\ 9\end{pmatrix} + \lambda \begin{pmatrix} 9\\ -5\end{pmatrix}$$
Aus der Gleichung für die X-Koordinate \(5=-4 + \lambda \cdot 9\) folgt, das \(\lambda\) in diesem Fall \(\lambda=1\) sein muss. Einsetzen von \(\lambda=1\) in die Gleichung für die Y-Koordinate \(a=9+ 1\cdot(-5)\) ergibt dann \(a=9-5=4\).
Nun fehlt noch das \(b\). Ich habe Dir ein paar Möglichkeiten für \(b\) in die Skizze eingezeichnet. \(b\) muss so liegen, dass der Vektor \(d_2\) (roter Pfeil) parallel zur Geraden \(g_1\) und damit zu \(d_1\) verläuft. man spricht hier von einer linearen Abhängigkeit. Das heißt es muss ein Wert \(\tau\) existieren, der die Gleichung:
$$d_2 = \tau \cdot d_1$$
erfüllt. Setzt man alles ein, was bekannt ist
$$ \begin{pmatrix} b\\ 3\end{pmatrix} = \tau \begin{pmatrix} 9\\ -5\end{pmatrix}$$
so folgt diesmal aus der Koordinatengleichung für Y: \(3 = \tau \cdot (-5)\), dass \(\tau\) hier \(=-3/5\) sein muss. Einsetzen von \(\tau\) in die Gleichung der X-Koordinate \(b=\tau \cdot 9 = (-3/5) \cdot 9 = -27/5=-5,4\). Also lautet die Gleichung für \(g_2\)
$$g_2: \space r(\mu) = \begin{pmatrix} 5\\ 4\end{pmatrix} + \mu \begin{pmatrix} -5,4\\ 3\end{pmatrix}$$
Gruß Werner