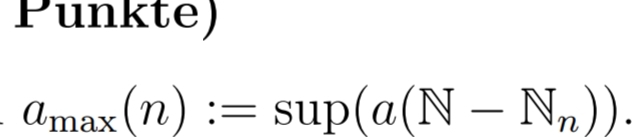Mir ist unklar was die Definition der folgenden Folge bedeuted.
Supremum ist klar, lediglich die Notation der natürlichen Zahlen verwirrt mich.
Wenn Nn die natürlichen Zahlen bis zu einem Index n sind, dann beinhaltet die Differenz auch nur endlich viele?
Kann mir das ein Analysis Kundiger verraten, wie man diese Definition zu verstehen hat?
a_(max)(n):= sup(a(N - N_(n) )).
mfG