Hi,
So, nach langem rechnen jetzt die Lösung.
Im folgenden beziehe ich mich auf diesen Link.
https://www.math.uni-hamburg.de/home/kiani/lehre/DGL2/anl4netz_d2_11.pdf
Zuerst wird das Problem entsprechend Seite 5 in zwei separate Probleme getrennt, und zwar so, dass jeweils ein Problem immer auf drei Rändern verschwindene Randwerte hat und nur auf einer Seite Randwerte ungleich Null besitzt.
Außerdem wird eine bilineare Eckenfunktion, s. Seite 6, eingeführt, um die Randbedingungen zu harmonisieren. Das hast Du in Deinem Lösungsansatz auch gemacht.
Für die Eckenfunktion muss gelten \( u(x,y) = u_E(x,y) = a + b x + c y + d x y \) an allen Ecken.
Anschließend wird das ursprüngliche Problem in ein Problem für die Funktion \( v(x,y) = u(x,y) - u_E(x,y) \) transformiert.
Aus den Anfangsbedingungen ergibt sich die Eckenfunktion zu \( u_E(x,y) = x \)
Mit Hilfe dieser Eckenfunktion müssen die Randbedingungen für die Funktion \( v(x,y) \) transformiert werden. Die daraus folgenden einzelnen Probleme ergeben sich damit zu
$$ (1) \quad \Delta v_1 = 0 \ \text{ mit } \ v_1(x,0) = x^2 - x \ \text{ und } \ v_1(x,1) = v_1(0,y) = v_1(1,y) = 0 $$ und
$$ (2) \quad \Delta v_2 = 0 \ \text{ mit } \ v_2(x,1) = x^2 - x \ \text{ und } \ v_2(x,0) = v_1(0,y) = v_1(1,y) = 0 $$
Auf Seite 3 bis 4 wird das Problem (1) gelöst:
Die Lösung ist auf Seite 4, direkt vor dem Beispiel A angegeben mit:
$$ (3) \quad v_1(x,y) = \sum_{k=1}^\infty b_k \sinh\left( \frac{k \pi}{L} (y - b) \right) \sin\left( \frac{k \pi}{L} x \right) $$ mit
$$ b_k = 2 \cdot \frac{ \beta_k }{ e^{-\frac{k \pi}{L} b } - e^{\frac{k \pi}{L} b} } $$
\( \beta_k \) sind Fourierkoeffizienten der ungerade fortgesetzten Funktion \( g(x) = x^2 - x \) und lauten \( \beta_k = \frac{4 [ (-1)^k -1 ]}{k^3 \pi^3} \)
Jetzt muss man nur noch \( L = b = 1 \) in die Lösung (3) des ersten Problems setzen.
Das zweite Problem wurde in Beispiel A gelöst, allerdings mit einer anderen Randbedingung.
Ersetzt man die im Beispiel angegebene Randbedingung \( g(x) = -\pi \sin(x) \) durrch \( g(x) = x^2 - x \) ergibt sich folgende Lösung für das zweite Problem
$$ v_2(x,y) = \sum_{k=1}^\infty \left[ \frac{ 4 \left[ (-1)^k - 1 \right]}{k^3 \pi^3 \sinh( k \pi)} \right] \sinh( k \pi y) \sin( k \pi x) $$
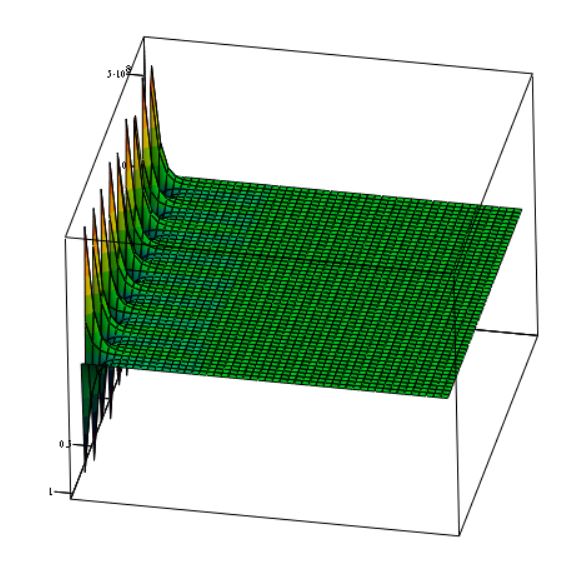
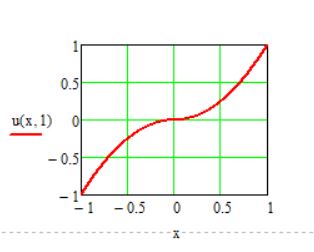
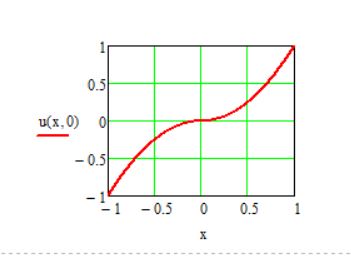
Die Gesamtlösung ergibt sich also zu
$$ u(x,y) = u_E(x,y) + v_1(x,y) + v_2(x,y) $$