Wir bezeichnen A_i als die Menge der natürlichen Zahlen, die durch i Teilbar sind.
Dabei sei i aus der Menge P:=N\{0} und J:=P U G = {2,4,6,...}.
Dann gilt
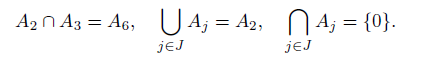
Die erste ist klar, denn nur A_6 ist durch A_2 und A_3 teilbar. Auch die zweite Menge ist denke ich klar, denn alle A_j lassen sich durch mindestens ein j teilen.
Bei der dritten Menge verstehe ich allerdings nicht wie man auf die 0 kommt.
Klar ist zwar, dass die Mengen A_j sich nicht durch alle j teilen lassen, sodass eine natürliche Zahl entsteht (z.B 2/4), aber woher kommt die Null? Bin ich überhaupt mit meinen Überlegungen richtig?
