Bestimmen Sie die Extrema der Funktion f(x, y) = x^2 + xy + y^2.

Question

hier ist die ganze Aufgabe:

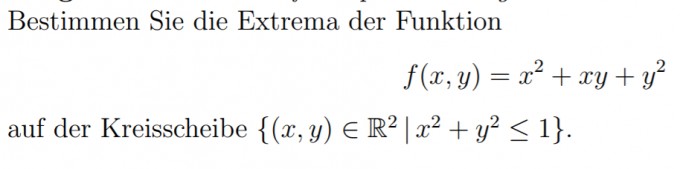
Ich habe das soweit gelöst.

aber ich weiß nicht wie ich am Ende bestimmen kann ob meine Punkte ein Maximum oder Minimum sind?

In der LÖsung steht Maximum... aber keine Begründung.

ganz zum Schluss, da weiß ich nicht, wo ich genau meinen Punkt einsetzen muss... ich muss ja eine hesse matrix bekommen, dann je nach det. oder Eigenwerten Maximum oder Minimum... oder geht das anders?

mfg

Answer 1

Hallo

 ja eigentlich den Punkt in die Hessematrix einsetzen, wenn das zu mühsam ist, den Wert mit Punkten darum vergleichen.

Gruß lul

Comments

also ich erhalte doch am Ende 3/2 wenn ich p_1 und p_2 in f einsetze... und das ist doch im grunde der abstand von p vom ursprung? und da dies der größte Abstand ist müssen ja p_1 und p_2 ein maximum sein? vielleicht war das also hier klar und deshalb gab es keine begründung. sonnst ja wie gesagt. p in die hesse und det anschauen... oder eben eigenwerte...

mfg

---

ja gut hab jetzt die aufgabe wiederholt... es ist ziemlich logisch. f(p) heißt wir bekommen den z koordinaten raus... und wenn z eben am kleinsten ist, muss es ein minimum sein, da max oder was anderes nicht mögl. ist. geht ja nicht weiter runter in die z-achse...  und bei max. eben andersrum.

Answer 2

einfacher gehts, wenn du das Problem in Polarkoordinaten löst:

f(r,φ)=r^2*(1+1/2 sin(2φ))

Leite nun nach r und phi ab!

Hier erkennt man gleich, wie sich die Funktion verhält, daher ob es sich um Maxima oder Minima handelt.

Comments

hier müsste das ohne polarkoordinaten gehen.

LUI sagte: "den Wert mit Punkten darum vergleichen." das muss ich machen... weiß aber nicht wie...

mfg