Wie löst man diese Gleichung: 1.8 ^ x = 2x

Question

1,8 ^ x = 2x

Mir fällt kein Weg ein, wie ich diese Gleichung lösen könnte.

Answer 1

Benutze den Taschenrechner, einen analytischen Weg zur Lösung gibt es nicht.

Answer 2

die Gleichung ist analytisch nicht lösbar. Benutze Näherungsverfahren,z.B eine Fixpunktiteration.

Man erhält mit Startwert x_1=1 recht zügig die Lösung x≈0.8

Answer 3

Näherungsverfahren von Newton: 
Berechnen der Nullstellen von f(x)  (f muss differenzierbar sein) 

f(x) = 1,8^x - 2x     ,  f '(x) = 1,8^x · ln(1,8) - 2

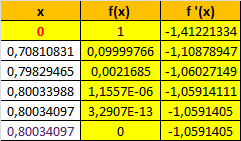
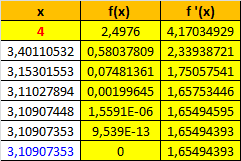
Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man - auch mit einem einfachen Taschenrechner -  immer bessere Werte mit der Formel$$x_{neu} =  x_{alt} - \frac{f(x_{alt})}{ f ' (x_{alt})}$$Du weißt allerdings i.A. nicht, ob du alle NS gefunden hast. Hier hilft oft eine Betrachtung der Extremwerte und der Krümmung.

Manchmal konvergiert das Verfahren nicht (wenn man für x_alt zum Beispiel eine Nullsstelle von f ' erwischt. Dann hilft oft ein anderer Startwert.
Je besser der Startwert, desto weniger Rechnung.

 

Gruß Wolfgang